Cs 10:15-11:00
The aim of this subject is to maintain the programming skills of the students through the solution of the programming tasks related to the Theory of Algorithms, and at the same time to facilitate a better understanding of the algorithms and the efficiency and complexity of them.
We are trying to give you interesting tasks that the solution will be of great benefit for every student. The number of tasks is 12, the total score is 60. The requirement is to submit at least 80% of the tasks by deadline (delay at most till the next lab with loss of 1 point) and reach at least 50% of the maximum total points is necessary for the assignment. You may correct your wrong code till the next lab. The program code must be uploaded in teams. The file name of the code starts with the job number, followed by the name of the student without spaces. E.g. Adrian Smith's 5th homework is named 5AdrianSmith.py, the next versions are named 5AdrianSmith1.py, 5AdrianSmith2.py and so on. Please never use space in filename and use differen filenames for new uploads as shown above. The program have to be written in Python 3. The following text must be added as a comment into every program code:
""" I encoded this program myself, did not copy or rewrite the code of others, and did not give or send it to anyone else. Your Name """
You have to follow the next rules. You must not submit or look at solutions or program code that are not your own. It is an act of plagiarism to submit work that is copied or derived from the work of others and submitted as your own. You must not share your solution code with other students, nor ask others to share their solutions with you. You must not ask anybody to write code for you. But many forms of collaboration are acceptable and even encouraged. It is usually appropriate to ask others for hints and debugging help or to talk generally about problem solving strategies and program structure. In fact, we strongly encourage you to seek such assistance when you need it. Discuss ideas together, but do the coding on your own.
Contents
- Pattern matching (2021-02-20 20:00)
- Nondeterministic finite automaton (2021-02-27 22:00)
- Breadth first search (BFS) (2021-03-06 22:00)
- Finding left derivation (2021-03-13 22:00)
- Effective verifier (2021-03-20 22:00)
- Euklidean algorithm (2021-03-27 22:00)
- Brute force (2021-04-03 22:00)
- Integer programming (2021-04-17 22:00)
- Bin packing (2021-04-24 22:00)
- Acrobats (2021-05-02 22:00)
- Union of intervals (2021-05-08 22:00)
- Binary search tree (2021-05-15 22:00)
1. Pattern maching
Deadline 2021-02-20 Saturday 20:00
- Write a program for comparing the simple matching and the quick search algorithms!
- The input for the program is given in a terminal command.
python3 1AdrianSmith.py text.text pattern
The program read the file text.text and search for the first occurrence of the given pattern in it. The command arguments can be read out from the inbuilt array sys.argv:
import sys print('Filename: {0}, pattern: {1}.'.format(sys.argv[1], sys.argv[2])) print("The name of this program has {0:2} characters".format(len(sys.argv[0]))) # {:2} would be equivalentThe sys.argv[0] contains the name of the program, the len() function gives the length of it. {0:2} means that the 0-th argument of the format()
function (that is the number of characters) is written into a two-character place in the output.
- For reading a file use the file functions, e.g.
f = open(filename, 'r') text = f.read().strip() f.close()
The strip() method cut down the unnecessary starting and ending white spaces.
- In your program you do not need to check if the specified text file exists or whether it actually contains text. The pattern is always at most as long as the text. The text contains lowercase letters of the English alphabet a-z and spaces. There are only lowercase letters in the pattern, but no spaces. According to the algorithms, the program allows the comparison of a single character of the text and the pattern, but does not use the Python 3 string functions except the len() function.
- Your program have to run the simple matching and the quick search algorithms with the given text and pattern. The output of the program specifies whether the pattern is in the text, at which character position and how many comparisons have been made to the first occurrence. Give 5 character space to the number of comparisons, and 4 character spaces to the position. The position number of the first character must be 1 (not 0). The output have to be look like this:
Simple matching: 2610 comparison(s), the pattern starts at 2321 Quick search: 270 comparison(s), the pattern starts at 2321
Specify the number of comparisons even if the pattern does not appear in the text:
Simple matching: 53610 comparison(s), no pattern Quick search: 5470 comparison(s), no pattern
- The input for the program is given in a terminal command.
- If you use the end="..." option in the print() function, the output of the next print() call will be continued in the same line.
- In Python 3 you may use special or accented lettes (e.g. you may write your name if it contains such letters of any language), but avoid such letters in the variable names, although it is possible.
- Try your program with the next downloadable text files and with the given patterns (of course in the test phase of your program, you may use your own very simple text files and patterns):
File Pattern 1.text overscrupulous 1.text zombies 2.text aaaaaaaaa 2.text bbbbbbbbb 2.text aaaaaaaab 2.text aaaaaaaba
2. Nondeterministic finite automaton
Deadline: 2021-02-27 22:00
- The program automaton.py simulates the running of a simple non-deterministic finite automaton.
- Download the program and run it with the command
python3 automaton.py word
where word is the word you want to recognize.
- The program uses the built-in set function to keep records of the currently available states in the computing tree of the non-deterministic finite automaton.
- Draw the automaton and determine what language does the automaton recognize? Please, write the answer in a comment into the code:
# The original program recognize the language: ...
Do not attach the figure.
- Download the program and run it with the command
- Change the description of the automaton in the file automaton.py between the lines
# the description of the automaton starts here
and
# the description of the automaton ends here
so that the program accepts the words that contain even number of letters a or contain the string algpr (or both)! So e.g. 'aaalgprbbb' and 'asdaefaa' are accepted but 'aaalgbb' is not.
3. Breadth first search (BFS)
Deadline: 2021-03-06 22:00
- Using the Breadth first search (BFS) algorithm known from the subject Combinatorics 1, we can find the shortest possible path in a graph between two given vertices. The task is to program this algorithm.
- The input of the algorithm is a simple directed graph, which is defined as follows in a text (.text) file:
- The first line of the file contains the natural numbers \(N\), \(M\), \(S\), \(T\) separated by spaces.
- The set of vertices of the simple directed graph \(\vec{G} = (V, \vec{E})\) is \(V = \{0, 1, 2, \ldots, N-1\}\).
- The number of edges is \(\left| \vec{E} \right| = M\).
- We would like to find the shortest directed path from the vertex \(S \in V\) to the vertex \(T \in V\) (\(S \ne T\)).
- The next \(M\) lines contain "\(U_i\) \(V_i\)" pairs of numbers. Such a pair represent the edge \((U_i, V_i) \in \vec{E}\). An edge appears only once in the file.
- If there is a path from \(S\) to \(T\), the program lists the vertices starting with \(S\) and finished with \(T\). If there is no path, it prints out "no path".
- The first line of the file contains the natural numbers \(N\), \(M\), \(S\), \(T\) separated by spaces.
- As a help we give a file graph.py, where we provide the input function of the graph and the output function of the path. So the search function search_path has to be written.
- The first parameter of this funcion is graph. This is the edge-list representation of the graph. The edge-list is given in a dictionary, where a list is belonging to every vertex. The elements in the list are vertices available by the outgoing edges. For example look at the graph of 6 vertices and 8 edges given in the next file
6 8 2 5 1 0 2 1 3 2 1 3 0 5 2 4 4 5 4 3
The next edge-list belongs to this graph
graph = {0: [5], 1: [0, 3], 2: [1, 4], 3: [2], 4: [5, 3], 5: []} - The next parameter of the function from_where gives the first vertex \(S\) and the third parameter to_where gives the last vertex \(T\).
- You may use the read_path function, which read out a path from a (not necessarily complete) BFS-tree between the from_where and to_where vertices. The BFS-tree is given in the parent dictionary, where the value assigned to a vertex is the number of its parent in the tree. For example in the case of
parent = {1: 2, 4: 2, 0: 1, 3: 1, 5: 4} from_where = 2 to_where = 5the shortest path is [2, 4, 5].
- When implementing the algorithm, it is not necessary to split the edges into classes (forward, backward,...), and not necessary to search in the whole graph, it is enough to find one shortest path.
- Buil-in list functions like append and pop(0) can be used to implement a queue. (But one may try the modul queue.)
- The first parameter of this funcion is graph. This is the edge-list representation of the graph. The edge-list is given in a dictionary, where a list is belonging to every vertex. The elements in the list are vertices available by the outgoing edges. For example look at the graph of 6 vertices and 8 edges given in the next file
- Test your program on the files graf1.text and graf2.text files, but also on other self-made input files!
4. Finding left derivation
Deadline: 2021-03-13 22:00
- The breadth first search is suitable for deriving a word in a context-free grammar.
- Consider the CF grammar \(G=(V,\Sigma,R,S)\), and construct the directed graph \(\vec{G}=((V\cup\Sigma)^*,\vec{E})\) where the vertices are the strings of terminal and non-terminal symbols. This graph has countably infinite number of vertices, but it is enough to search in a finite part of it for finding a derivation of a word.
- The graph \(\vec{G}\) contains the edge \((\alpha, \beta)\) if and only if there is a left-derivation step from the string \(\alpha \in (V \cup \Sigma)^*\) to the string \(\beta \in (V \cup \Sigma)^*\), in other words we get \(\beta\) if we apply a substitution rule from \(R\) on the first non-terminal symbol of \(\alpha\). Formally \begin{equation*} (\alpha, \beta) \in \vec{E} \Longleftrightarrow \exists w \in \Sigma^* \; \exists \gamma, \delta \in (V \cup \Sigma)^* \; \exists A \in V \colon (A \rightarrow \delta) \in R, \alpha = wA\gamma \textrm{ and } \beta = w\delta\gamma. \end{equation*}
- In this graph the left derivations of the word \(w \in L(G)\) are exactly the \(S \leadsto w\) paths, where \(S \in V\) is the start variable. All edges of a path correspond to a rule applied on the leftmost non-terminal symbol. We want to find such a path in this task.
- We give the skeleton of the program in the file CF.py. The only command line argument of this program is a word to derive. The prgram prints out the derivation to the standard output.
The separation of the terminal and non terminal symbols is solved by a simple method: all capital letters A to Z of the English alphabet are possible non-terminal symbols while all other characters are terminal.
- The CF grammar is represented by the class Grammar. The start symbol is given to the constructor argument start_variable. Complete the add_rule method such that it adds the left and right side of a rule to the language. If necessary, modify the __init__ constructor creating a suitable data structure to store the rules.
- The derive method gets a word as a parameter and returns a left derivation in a list. If there is surely no such derivation, it returns False. To do this, it uses the breadth first search (presented in the previuos task) algorithm realized by the private function _bfs_search. Because the graph is now infinite, we can not list all edges. Instead, we use the _next method producing a list of vertices that can be reached on an edge from the string vertex in the graph.
Complete the _next method such that it returns a list of words which are available from the received string vertex by a single left derivation rule. For example, if the grammar is \begin{equation*} S \to aSB \mid bSA \mid \epsilon, \quad A \to aA \mid \epsilon, \quad B \to bB \mid \epsilon, \end{equation*} then
self._next('aSbbB') == ['aaSBbbB', 'abSAbbB', 'abbB'] - Let's try the program and find derivation to some given words. Please, answer the following questions in a """-type comment at the end of the code! (1) What language is specified in the file CF.py? (2) What happens when we give a word to the program that is not in the language? (3) A non mandatory question and task: how could we change the program code to handle this case? Do it!
- The isinstance() function and islower(), extend(), append() methods might help.
5. Effective verifier
Deadline: 2021-03-20 22:00
- The task in this week is to write a Python program that implements an effective verifier algorithm deciding on a given graph that a given sequence of numbers represents a Hamiltonian cycle in the graph. (This task is preparing for a later topic in Algorithm theory where you will learn that the language HAM of graphs containing Hamiltonian cycles is in NP.)
- It is easy to decide for a graph and a sequence of numbers that the sequence forms a Hamiltonian cycle in the graph – one just have to check that each vertex occurs exactly once and there are edges between each pair of consecutive vertices, and between the first and last vertex.
- The program receives the input in the form of command line arguments.
python3 5AdrianSmith.py graf.text witness.text - The first input (in the example graf.text) is a non directed simple graph that we enter in a text (.text) file
- There are two natural numbers separated by spaces in the first line \(N\) and \(M\) where
- the simple graph \(G = (V, E)\) has \(N\) vertices, namely \(V = \{0, 1, 2, \ldots, N-1\}\),
- and has \(M\) edges, that is \(\left| E \right| = M\).
- The next \(M\) lines of the file contains pairs of numbers \(U_i, V_i\). One such pair corresponds to a (non directed) edge \((U_i, V_i)\). Every edge is listed only once in the file.
- To process the input we recommend modifying the code of the appropriate part of the 3rd task. Note that the first line of the file here does not contain the vertices \(S\) and \(T\). Since the edges of the graph are not directed, you may want to add edges to the edge list of both endpoints!
- There are two natural numbers separated by spaces in the first line \(N\) and \(M\) where
- The second input of the program is a sequence of integers. The task of the program is to decide whether the sequence of numbers represents a Hamiltonian cycle in the graph (verify whether the sequence is a witness of the existence of a Hamiltonian cycle).
- If it is a Hamiltonian cycle (a witness) print the text
witness
otherwise print
not a witness
- Try the program with the file graf.text and with the next input files:
Filename Expected output t1.text witness t2.text not a witness t3.text not a witness t4.text not a witness t5.text witness t6.text not a witness t7.text not a witness
6. Euklidean algorithm
Deadline: 2021-03-27 22:00
- The Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor of two numbers. If the input \(a, b \in \mathbb{Z}^+\) are two binary numbers, then the length of input is \(O(\log a + \log b)\), and the Euclidean algorithm calculate the value \(\mathop{\mathrm{gcd}}(a, b)\) in at most \(O(\log a + \log b)\) steps.
- In the file euklidean.py a part of a program is given which plot the heat map of the function \(\log a + \log b\) on the \((a, b)\) coordinate-plane with the matplotlib Python package. The values of \(a\) and \(b\) are the integer numbers between \(1\) and \(100\). The heat map shows the value of the numbers with the colors of the rainbow (violet, indigo, blue, green, yellow, orange, red). The older versions of the matplotlib package uses violet for small and red for big numbers, but in the new versions the colors are changing from violet to yellow only.
- Modify the program to show the running of the euclidean algorithm! Plot three heat maps side by side in a window similar to one of the following. With the new version of matplotlib installed on your computer the result of the home work looks like this:
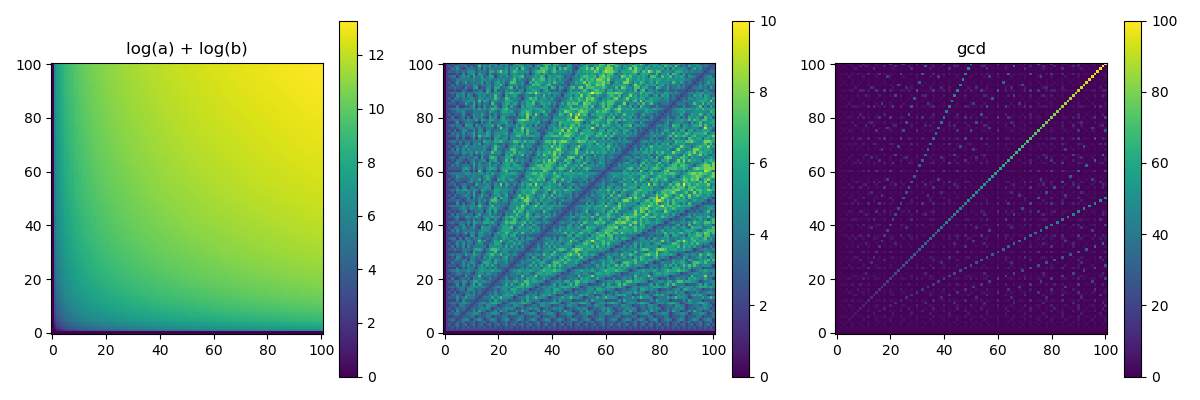
with the old version like this
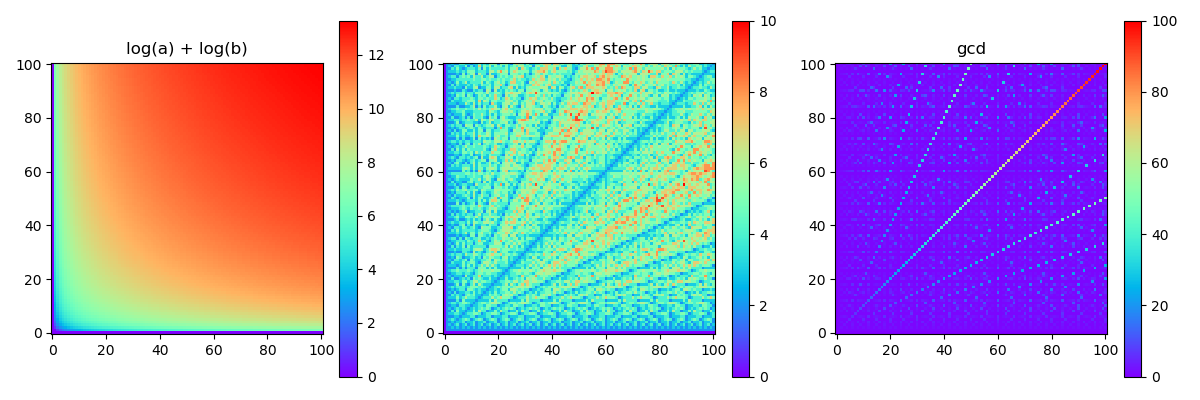
The following functions should be shown on the heat maps:
- The first heat map shows the function \(\log_2 a + \log_2 b\), which is generated by the program downlaodable above.
- The second heat map shows the number of steps of the Euclidean algorithm on each pair \((a, b)\). On the number of steps we mean: how many divisions with reminder made on \((a_i, b_i)\) pairs or decide to stop
- The third heat map shows the value \(\mathop{\mathrm{gcd}}(a, b)\).
- The subplot function of matplotlib package can be used to display multiple figures. The argument of this function is a 3-digit number \(nmk\), where the \(n\) is the number of rows, \(m\) is the number of columns of subfigures on the canvas. The third \(k\) is the index of the subfigure, which starts at 1 in the upper left corner and increases to the right. For example
plt.subplot(132)means that the canvas has 3 subfigures in a row, and all the results of the function calls of plt appear on the second subfigure.
7. Brute force
Deadline: 2021-04-03 22:00
- One possible way to solve NP-complete problems is to use "brute force." In this approach, we generate all possible witnesses according to the input and check them one by one. If we find a good witness, then the input is in the tested language, but if none of the generated witnesses are good, then the input is certainly not an element of the language. Of course, we cannot expect this procedure to solve the problem in polynomial time.
- The language \(\textrm{IND}\) consists of pairs \((G, k)\) where a simple non-directed graph \(G\) has \(k\) independent vertices (an independent set is also called stable set, coclique or anticlique). It is a good witness for \((G, k) \in \textrm{IND}\) if there is a set \(F \subseteq V(G)\) of \(k\) independent vertices. If \(|V(G)| = n\), then it is possible to decide in \(O(n^2)\) time on a set \(F\) of points if there is no edge between the points of \(F\).
- Write a program that determines whether \((G, k)\) is in the \(\textrm{IND}\) language. \(G\) and \(k\) is described in a file given in a command line argument. If you find an independent \(k\)-element vertex set, write it to the standard output. Otherwise indicate that there is no independent set of \(k\) elements in the graph.
- In the file ind.py a function read_graph is given which read the edges of \(G\) and the number \(k\) from the file given in the command line argument. The format of the input file and the return values described in the docstring of the source code.
- Generate all \(k\)-element combinations of the vertex set \(\{0, 1, \ldots, n - 1\}\) of the graph and decide if any of them is independent. Stop the search if you find an independent set and write it to the standard output. If there is no independent set indicate on the standard output that there is no independent \(k\)-set.
- To help coding we provide the function combinations which write the 3-element combinations of the set \(\{0, 1, \ldots, 9\}\) to the standard output using the itertools package. (Of course, use the ideas of this function only, not the function itself.)
- Try your program with the next files! For the inputs belonging to the language \(\textrm{IND}\) we give an independent set as a verifier. Of course any other independent set will be accepted as a witness.
File Independent set ftln1.text 1 2 7 ftln2.text no ftln3.text 0 4 9 11 12 14 19 ftln4.text no ftln5.text 2 5 18 29 39 ftln6.text no
8. Integer programming
Deadline: 2021-04-17 22:00
- Another known method for solving NP-complete problems is to bring the problem back to another well-known NP-complete problem. If we have an effective heuristic solver for a well-known problem, we can usually achieve better results than with brute force. In this exercise, we slightly extend the previous week's IND problem, and solve the MAXIND problem using integer linear programming tools. In IND we had to decide if an independent \(k\)-set in a given graph exists or not. In MAXIND we have to find the max value of \(k\) for which an independent \(k\)-set exists. We solve the integer linear program with the PuLP Python package. Install it with the built-in package manager pip (or pip3) using the command
pip install pulp
- In the file pulpexample.py we give a simple example for solving the integer programming problem \begin{align*} \max\, x_0 + x_1,\\ \text{where } x_0, x_1 \in \mathbb{Z},\\ x_0 \ge 0, \\ x_1 \ge 0, \\ 2 x_0 + x_1 \le 10, \\ x_0 + 2 x_1 \le 10, \end{align*} and write out the solution to the standard output. Let's study this program! The PuLP package documentation can help you understand it.
- Let's write a program to solve the MAXIND problem!
- Read the input of the problem, that is the simple non-directed graph \(G\) and \(k\) from a file having the same format as in the previous exercise, although \(k\) will not be used here. As with the previous task, the program will receive the file name as a command line argument.
- Let's define MAXIND as an integer programming task.
- Program the integer programming problem with the PuLP package and call the solver. (Make sure that both the problem and the variables are given a unique name which is a character string, because PuLP identify them in this way when they are given to the external solver. If the names of the variables are not unique, we will receive an error message.)
- Write the size of the maximum independent set and the elements of such a set to the standard output. PuLP returns the value of the objective function as a floating-point number, so round it before printing.
- Run the program with the inputs of the previous task. Although we are now solving a more demanding task, the files ftln2.text, ftln4.text, ftln6.text show that integer programming is much faster than brute force.
9. Bin packing
Deadline: 2021-04-24 22:00
- In the bin packing task, we have to determine the minimum number of \(1\) capacity bins into which taken the given \((s_i)_{i = 1}^n\), \((0 < s_i \le 1)\) weights fit. The problem is NP-complete, so an effective solution (according to our current knowledge) is not available, but several approximation algorithms have been created for it. In this task, the aim is to examine some approximate heuristics.
- In the file binPack.py we have provided a framework program that examines the lower limit and three approximation algorithms for the bin packing problem at a given input:
- The value of OPT is the ceiling of (the smallest integer greater or equal than) the total weight of objects, which is the lower limit for the required number of bins.
- The first-fit (FF) algorithm puts all packs in the first bin where it fits.
- The first-fit decreasing (FFD) algorithm is similar to FF, but first it sorts the packs in descending order.
- The best-fit (BF) algorithm puts all objects in the bin where the least space is left. (This is already written in the program, study it.)
- Modify the binPack.py file and finish the program!
- Implement the first_fit_pack function of the FF algorithm.
- Implement the ffd_pack function of the FFD algorithm. Be careful as Python passes the lists by reference to the function, so do not sort the list in its place, because it modifies the original list.
- In the program a list named packs is given. Change it for a list of random 1000 element list of numbers between 0 and 1, and call the packing functions with these values.
- Run the program a few times! Compare, how the algorithms work on the generated random inputs!
10. Acrobats
Deadline: 2021-05-02 22:00
- Circus acrobats are standing on each other's shoulders to create a larger tower (there will be only one acrobat on each level in the tower). For aesthetic and practical reasons, one person's shoulders can stand only lower and lighter acrobat. Our task is to determine the number of possible most people in a tower.
- In the file acrobat.py we have provided an example program that reads the acrobats from the file named in the command line argument, and then prints them in a non-incremental order to the standard output. The file format is as follows:
- The first line of the file contains a single positive integer \(N\), the number of acrobats.
- The file \(i + 1\)-st line gives the height and weight of the \(i\)-th acrobat.
- The function read_acrobats reads the data of acrobats and returns with the list of Acrobat class instances. The acrobats have the id (identifier), height and weight attributes and a may_stand_on method, which determines whether an acrobat can stand on an another.
- Use Dynamic Programming (see e.g. in Info2 the exchange or partition problem) to determine the number of the most people in the tower complies with the rules. Let you try the program with the following inputs. We have also given the number of the most possible people in the tower:
Input Max tower cirkusz1.text 2 cirkusz2.text 3 cirkusz3.text 1 cirkusz4.text 100 cirkusz5.text 15 cirkusz6.text 37
11. Union of intervals
Deadline: 2021-05-08 22:00
- Given \(N\) closed intervals \([A_1, B_1], [A_2, B_2], \ldots [A_N, B_N]\), where \(A_i\) and \(B_i\) are natural numbers. We want to dermine the total length of the intervals, precisely the measure of the domain \(\bigcup_{i = 1}^N [A_i, B_i]\).
- We provide an example program interval.py that reads the intervals from the file named in the command line argument. The file format is as follows:
- The first line contains one natural number, the number of intervals \(N\).
- There are \(A_i\) \(B_i\) pairs in the next \(N\) lines. These are the starting and the endpoint of the \(i\)-th interval, where \(0 < A_i < B_i\).
- The function read_intervals reads the intervals and return a list of Interval objects. The class Interval has two properties: start and end, these are the bounderies of the interval.
- Complete the code of the measure function, such that it calculates the total length of the intervals, that is the measure of the union of the intervals. Let's try to achieve the efficient algorithm of \(O(N \log N)\) steps.
- Try the program on the following inputs. The efficient algorithm of \(O(N \log N)\) steps runs on each of the following inputs in a few seconds. In addition to the inputs, we have given in the table the total length of the intervals.
Input Measure interv1.text 9 interv2.text 596 interv3.text 6541 interv4.text 94581377 interv5.text 632741470
12. Binary search tree
Deadline: 2021-05-15 22:00
- In this task a binary search tree data structure will be programmed. A part of the implementation of the search tree is given in the program bintree.py.
- The binary tree is represented by the BinaryTree class. The root of the tree is contained by the root attribute. If the tree is empty, the value of this attribute is None, otherwise the root is an instance of the class TreeNode.
- The nodes are the instances of the TreeNode class. The values of the left and right attributes are None, if no child is there, or the TreeNode instance representing the child node.
- The methods of the BinaryTree class are insert, search_key, level, preorder_walk. They check if there is a root of the tree and then call on the appropriate recursion methods of the TreeNode class.
- The common recursive part of the insert and search_key methods is the search_node method of the TreeNode class. This searches in the tree to find the key value received as a parameter and returns the node where the search stops. This is the node that contains the value we are looking for, or if the key value is not in the tree, the node which the key value node should be the child of.
- The main program reads integers from the file given as a command line argument, and then inserts them into the binary tree. Then print out the values in the preorder order to the standard output and calculate the number of tree levels.
- Complete the file bintree.py with the missing parts!
- Insert the given key into the tree in the insert method of the BinaryTree. You may use search_node method of TreeNode, which returns the node that either contains the value you are looking for or the value you are looking for is to be inserted as the direct child of the node. The use of this method is also illustrated by the search_key method of the BinaryTree class. Make sure that the insertion works on an empty binary tree or if a node is already contains the value you want to insert. In the latter case, the insertion is idempotent.
- Print out the values of the tree with a recursion in the preorder order to the standard output in the preorder_walk method of TreeNode.
- Using recursion, determine the number of levels of the tree in level method of TreeNode.
- Test the program with the files binfa1.text, binfa2.text, binfa3.text, binfa4.text, binfa5.text. Test some of your own testfiles!

