A tárgy célja az Algoritmuselmélet című tárgy tematikájához kapcsolódó programozási feladatok megoldásán keresztül a hallgatók programozási képességeinek szinten tartása, és egyúttal az algoritmusok működésének, hatékonyságának, bonyolultságának... jobb megértése.
A tárgy 1 kredites, ami összesen 30 óra, azaz heti 2-3 óra programozási munka elvégzését kívánja. Olyan feladatokat igyekszünk adni, melyek érdekesek lesznek mindenki számára, és amelyek megoldása sok haszonnal fog járni. A feladatok száma 12, összpontszáma 60. Követelmény a feladatok legalább 80%-ának határidőre való leadása (illetve 1 pont elvesztése mellett legföljebb 1 héttel későbbi, késedelmes leadása) és a feladatokra kapható maximális összpontszám legalább 50%-ának elérése. A hibásan megoldott feladat az eredmény kihirdetése utáni 1 héten belül javítható. A feladatok megoldását egyelőre az alg.progfel@gmail.com címre csatolmányként kell elküldeni (ez várhatóan változni fog a szemeszter köben), külön fájlban a Python programkódot. A programfájl neve a feladat sorszámával kezdődjön, folytatásul a hallgató neve legyen szóközök nélkül, pl. Kovács Jutka 5-dik házi feladatát 5KovacsJutka.py, adatfájlját 5adatKovacsJutka.txt néven küldje el. Minden feladatot Python3-ban kell megoldani! Minden házi feladat kísérő levelébe az alábbi szöveget kell írni:
E programot magam kódoltam, nem másoltam vagy írtam át más kódját, és nem adtam át másnak! Aláírás saját névvel
Az, hogy a program kódját mindenkinek magának kell beírnia, programkódot átadnia, mástól kérnie és elfogadnia, letöltenie és átírnia nem szabad, nem zárja ki az együtt gondolkodás vagy a segítségkérés lehetőségét! Konzultáció is kérhető, személyes is.
Tartalomjegyzék
- Mintaillesztés (2020-02-23 24:00)
- Nemdeterminisztikus véges automata (2020-03-03 24:00)
- Szélességi keresés (2020-03-08 24:00)
- Bal-levezetések keresése (2020-03-15 24:00)
- Hatékony tanúsítvány (2020-04-01 24:00)
- Euklideszi algoritmus (2019-04-07 24:00)
- Nyers erő (2020-04-16 24:00)
- Egészértékű programozás (2020-04-22 24:00)
- Ládapakolás (2020-04-29 24:00)
- Akrobaták (2020-05-06 24:00)
- Intervallumok uniója (2020-05-13 24:00)
- Bináris keresőfa (2020-05-20 24:00)
1. Mintaillesztés
Határidő: 2020-02-23 vasárnap 24:00
- Írjunk programot az órán tanult két mintaillesztési algoritmus összehasonlítására!
- A program a bemenetet parancssori argumentumok formájában kapja meg, a következőképp indítható:
python3 1KovacsJutka.py szoveg.txt minta
Ekkor a program olvassa be a szoveg.txt szöveges fájl tartalmát, és keresse meg benne a minta első előfordulását. A parancssori argumentumok lekérdezhetőek a beépített sys.argv tömbben, ami a következő 3-soros mintaprogrammal kipróbálható:
import sys print('Fájlnév: {0}, minta: {1}.'.format(sys.argv[1], sys.argv[2])) print("E program neve {0:2} betű".format(len(sys.argv[0]))) # {:2} is ugyanazA sys.argv[0] értéke az éppen futtatott Python program neve, len() függvény annak hosszát adja meg, a {0:2} azt jelenti, hogy a format függvény 0-dik argumentumát kell beírni 2 karakternyi helyre. Ezt a lehetőséget használjuk majd a program megírásakor is.
- Fájl beolvasására javasoljuk a Python fájlkezelő függvényeit, például az alábbi módon:
f = open(fajlnev, 'r') szoveg = f.read().strip() f.close()
A strip() metódus segítségével levághatjuk az esetlegesen előforduló sorvége karaktereket és felesleges szóközöket a bemenet elejéről és végéről.
- Python3-ban a programba bárhol írhatunk ékezetes betűket is, de a fájl utf-8 kódolású legyen. Lehetnek a változónevekben is ékezetes karakterek, de ezt inkább kerüljük el!
- Nem kell ellenőrizni, hogy a megadott szövegfájl létezik-e, vagy hogy valóban szöveget tartalmaz-e. A minta mindig legfeljebb olyan hosszú, mint a szöveg. A szöveg csak az angol ábécé a–z kisbetűit és szóközöket tartalmaz. A mintában csak kisbetűk vannak, szóköz nincs. Az algoritmusoknak megfelelően a programban csak a szöveg és a minta egy-egy karakterének összehasonlítása megengedett, de a Python sztringkezelő függvényeinek használata nem, kivéve a len() függvényt.
- Futtassuk le az egyszerű mintaillesztő algoritmust és a gyorskeresést (quick search) a megadott szöveggel és mintával. A program írja ki, hogy előfordul-e a minta a szövegben, és hány összehasonlítást végeztünk az első előfordulás megkereséséig. A keresések számára 5 karakter helyet biztosítsunk, a találat helyére 4 karaktert a formázott kimenetben.
Lassú: 3260 összehasonlítás, találat helye: 3568 Gyors: 397 összehasonlítás, találat helye: 3568
Akkor is adjuk meg az összehasonlítások számát, ha a minta nem fordul elő a szövegben:
Lassú: 5239 összehasonlítás, nincs találat Gyors: 768 összehasonlítás, nincs találat
- A program a bemenetet parancssori argumentumok formájában kapja meg, a következőképp indítható:
- Python3-ban az end="..." opcióval érhető el, hogy a print() függvény ne egy új-sor-karakterrel fejezze be a kiírást, hanem az opcióban megadott karakterlánccal, így a következő print() hívás kimenete ugyanabban a sorban folytatódik. Például print("szöveg", end=" ") kiírja a szöveget, szóközt tesz a végére, és a következő print() hívás kimenetét ott folytatja.
- Próbáljuk ki a programot az alább letölthető két szövegfájllal és a megadott mintákkal! (Tesztelési fázisban természetesen érdemes saját text fájlokkal és mintákkal kísérletezni.)
Fájlnév Minta 1.text overscrupulous 1.text zombies 2.text aaaaaaaaa 2.text bbbbbbbbb 2.text aaaaaaaab 2.text aaaaaaaba
2. Nemdeterminisztikus véges automata
Határidő: 2020-03-03 24:00
- Az automata.py fájlban megadtunk egy programot, ami egy egyszerű nemdeterminisztikus véges automata futását szimulálja.
- A programot a
python3 automata.py szo
paranccsal futtathatjuk, ahol a szo a felismerni kívánt szó.
- A program a Python beépített halmazkezelő függvényeit használja, hogy a nemdeterminisztikus véges automata számítási fájában aktuálisan elérhető állapotokat számon tartsa.
- Rajzoljuk le az automatát, és magyarázzuk meg saját szavainkkal: (1) hogyan szimulálja a program a működését, (2) milyen nyelvet ismer fel az automata? (A kísérőlevélben csak ez utóbbi két kérdésre kell válaszolni, a rajzot nem kell mellékelni.)
- A programot a
- Módosítsuk az automata leírását az automata.py fájlban
# Itt kezdődik az automata leírása:és
# Idáig tart az automata leírása.
sorok között úgy, hogy a program épp azon szavakat fogadja el, melyek páros sok a betűt tartalmaznak, vagy tartalmazzák az algel karaktersorozatot (vagy akár mind a kettőt)! Például az 'aaalgelbbb' és 'asdaefaa' szavakat elfogadja, az 'aaalgbb' szót nem.
3. Szélességi keresés
Határidő: 2020-03-08 24:00
- A Kombinatorika és gráfelmélet 1. tárgyból megismert szélességi keresés algoritmussal megtalálhatunk egy lehető legkevesebb élből álló utat egy gráfban két adott csúcs között. A feladat ennek az algoritmusnak a beprogramozása.
- Az algoritmus bemenete egy irányított egyszerű gráf, amit a következő módon adunk meg egy szöveges (.text) fájlban:
- A fájl első sorában az \(N\), \(M\), \(S\) és \(T\) természetes számok találhatóak szóközökkel elválasztva.
- A \(\vec{G} = (V, \vec{E})\) irányított egyszerű gráf csúcsai a \(V = \{0, 1, 2, \ldots, N-1\}\) számok.
- Az élek száma \(\left| \vec{E} \right| = M\).
- Az \(S \in V\) csúcsból szeretnénk egy legkevesebb élből álló utat keresni a \(T \in V\) csúcsba (\(S \ne T\)).
- A fájl további \(M\) sora rendre \(U_i\), \(V_i\) számpárokat tartalmaz. Egy ilyen számpár megfelel egy \((U_i, V_i) \in \vec{E}\) élnek. Egy él csak egyszer szerepel a fájlban.
- A program, ha létezik út az \(S\) és \(T\) csúcsok között, akkor az \(S\) csúccsal kezdve sorban megadja annak csúcsait a \(T\) csúcsig. Ha nincs út, akkor kiírja, hogy „Nem létezik út!”.
- A fájl első sorában az \(N\), \(M\), \(S\) és \(T\) természetes számok találhatóak szóközökkel elválasztva.
- Segítségképp megadjuk a graf.py fájlban a gráfot beolvasó és a megtalált utat kiíró függvényt, így csak magát a keresést kell megvalósítani az utat_keres függvényben.
- A függvény első, graf paramétere a gráf éllistás ábrázolása. Az éllistát egy szótárral (dictionary) adjuk meg, melyben minden csúcshoz egy lista tartozik. A lista elemei a kimenő éleken elérhető csúcsok. Például az alábbi fájlban leírt gráfhoz
6 8 2 5 1 0 2 1 3 2 1 3 0 5 2 4 4 5 4 3
tartozó éllista
graf = {0: [5], 1: [0, 3], 2: [1, 4], 3: [2], 4: [5, 3], 5: []} - A honnan paraméter az út első, \(S\) csúcsát, míg a hova paraméter az út utolsó, \(T\) csúcsát adja meg.
- A megoldáshoz felhasználható az utat_kiolvas függvény, ami egy (nem feltétlenül teljes) szélességi fából kiolvas egy utat a honnan és hova csúcsok között. A szélességi fát a szulo szótárban kell megadni, ahol az egyes csúcsokhoz rendelt érték a szülőjük azonosítója a szélességi fában. Például
szulo = {1: 2, 4: 2, 0: 1, 3: 1, 5: 4} honnan = 2 hova = 5esetén egy legrövidebb út [2, 4, 5].
- Az algoritmus megvalósításánál nem szükséges az éleket fa-, előre-, vissza- és keresztélekre bontani, mivel ezek nélkül is kiolvasható egy legrövidebb út. Az egész gráfot sem kell bejárni, elég akkora részét, hogy meg lehessen találni egy legrövidebb utat.
- Várakozási sor megvalósítására alkalmasak a beépített listák append és pop(0) függvényei, de ki lehet próbálni a Python 3 queue modulját is.
- A függvény első, graf paramétere a gráf éllistás ábrázolása. Az éllistát egy szótárral (dictionary) adjuk meg, melyben minden csúcshoz egy lista tartozik. A lista elemei a kimenő éleken elérhető csúcsok. Például az alábbi fájlban leírt gráfhoz
- Próbáljuk ki az elkészült programot a graf1.text és graf2.text bemenetekre, de teszteljük más, saját készítésű teszbemeneteken is!
4. Bal-levezetések keresése
Határidő: 2020-03-15 24:00
- A szélességi keresés arra is alkalmas, hogy egy környezetfüggetlen nyelvtanban levezetést adjuk egy szóhoz.
- Tekintsük a \(G = (V, \Sigma, R, S)\) CF nyelvtant, és képezzük a \(\vec{G} = ((V \cup \Sigma)^*, \vec{E})\) irányított gráfot, melynek csúcsai a terminális és nemterminális szimbólumokból képzett sztringek. Ennek a gráfnak megszámlálhatóan végtelen csúcsa van, de ezek közül elég lesz véges sokat bejárni, hogy egy levezetést találjunk.
- A \(\vec{G}\) gráf akkor és csakis akkor tartalmazza az \((\alpha, \beta)\) élt, ha az \(\alpha \in (V \cup \Sigma)^*\) sztringből egy bal-levezetési lépéssel (az \(\alpha\) sztringben legelőször előforduló nemterminális szimbólumra egy levezetési lépés alkalmazásával) elérhető a \(\beta \in (V \cup \Sigma)^*\) sztring. Formálisan, \begin{equation*} (\alpha, \beta) \in \vec{E} \Longleftrightarrow \exists w \in \Sigma^* \; \exists \gamma, \delta \in (V \cup \Sigma)^* \; \exists A \in V \colon (A \rightarrow \delta) \in R, \alpha = wA\gamma \textrm{ és } \beta = w\delta\gamma. \end{equation*}
- Ebben a gráfban a \(w \in L(G)\) szó bal-levezetései épp az \(S \leadsto w\) utak, ahol \(S \in V\) a kezdő változó. Az út minden éle megfelel valamelyik \(R\)-beli szabály alkalmazásának a legbaloldalibb nemterminális szimbólumra. A feladatban egy ilyen utat szeretnénk megkeresni.
- A cf.py fájlban megadtuk a levezetést kereső program vázát. A program egyetlen parancssori argumentumot vár, a levezetendő szót. A megtalált levezetést a standard kimenetre írja.
A programban egy egyszerű módszerrel oldottuk meg a terminális és nemterminális szimbólumok különválasztását: az angol ábécé minden A–Z nagybetűjét lehetséges nemterminális szimbólumnak tekintjük, míg az összes többi karaktert terminálisnak.
- A CF nyelvtant a Nyelvtan osztállyal reprezentáljuk, amely kezdőszimbólumot a kezdovaltozo konstruktor argumentumban kapja meg. Egészítsük ki az add_szabaly metódust úgy, hogy a megadott bal és jobb oldalú levezetési szabályt hozzávegye a nyelvtan szabályaihoz. Ha szükséges, módosítsuk az __init__ konstruktort úgy, hogy létrehozza a szabályok tárolására alkalmas adatstruktúrát.
- A levezet metódus a paraméterül kapott szó egy bal-levezetését adja vissza egy listában. Ha biztosan nincs ilyen, akkor a False értékkel tér vissza. Ehhez segítségül hívja az előző feladatban bemutatott szélességi keresést, amit a _szelessegi_kereses privát metódus valósít meg. Mivel a gráf most nem véges, nem állíthatjuk elő az éllistáját. Ehelyett a _rakovetkezo metódust használjuk, ami egy adott csucs sztringhez előállítja az onnan kimenő élen elérhető csúcsait a gráfnak.
Egészítsük ki a _rakovetkezo metódust úgy, hogy a paraméterül kapott csucs sztringből megengedett bal-levezetési lépéssel kapható szavak listáját adja vissza! Például, ha a nyelvtan
\begin{equation*} S \to aSB \mid bSA \mid \epsilon, \quad A \to aA \mid \epsilon, \quad B \to bB \mid \epsilon, \end{equation*}
akkor
self._rakovetkezo('aSbbB') == ['aaSbbbB', 'abSAbbB', 'abbB'] - Próbáljuk ki a programot, és keressünk levezetést néhány általunk választott szóhoz! A kísérőlevélben válaszoljunk a következő kérdésekre! Milyen nyelvet határoz meg a cf.py fájlban megadott nyelvtan? Mi történik, ha olyan szót adunk meg a programnak, ami nincs benne a nyelvben?
- A szélességi keresés során a \(\vec{G}\) gráf nagyon sok csúcsát előállítjuk és bejárjuk, mire meg tudunk találni egy utat az általunk kívánt szóhoz. Gondolkozzunk el azon, hogy hogy lehetne a gráfnak csak kisebb részét bejárni, és ezzel hatékonyabbá tenni a programot (ezt a részt már nem kell leprogramozni)!
5. Hatékony tanúsítvány
Határidő: 2020-04-01 24:00
- Az algoritmuselmélet tárgyban fognak vele találkozni/találkoztak vele, de a Turing gépek jegyzetben is szerepel, hogy a Hamilton-körrel rendelkező gráfok nyelvére \(\textrm{HAM} \in \textrm{NP}\) teljesül. A bizonyítást a tanú-tétel segítségével végezhetjük el úgy, hogy egy – a Hamilton-kör létezését mutató – hatékony tanúsítványt megadunk. Ennek alapötlete, hogy egy adott gráfhoz megadunk egy számsorozatot, ami a feltételezett Hamilton-kör csúcsait jelöli egy körnek megfelelő sorrendben. Ha a számsorozatban minden csúcs pontosan egyszer fordul elő, valamint a számsorozatban egymásutáni csúcsok, illetve az első és az utolsó csúcs szomszédosak a gráfban, akkor a tanusítvány bizonyítja a Hamilton-kör létezését.
- A feladat egy olyan Python program írása, mely a fenti (és a jegyzetben is vázolt) hatékony tanúsítvány algoritmusát valósítja meg: eldönti egy adott (gráf, számsorozat) párról, hogy az adott számsorozat egy Hamilton-kört reprezentál-e a gráfban.
- A program a bemenetet parancssori argumentumok formájában kapja meg.
python3 5KovacsJutka.py graf.text tanu.text
módon indítani.
- Az első bemenet (a példában graf.text) egy irányítatlan egyszerű gráf, amit a következő módon adunk meg egy szöveges (.text) fájlban:
- A fájl első sorában az \(N\), \(M\) természetes számok találhatóak szóközökkel elválasztva, ahol
- a \(G = (V, E)\) egyszerű gráf csúcsainak halmaza \(V = \{0, 1, 2, \ldots, N-1\}\),
- az élek száma \(\left| E \right| = M\).
- A fájl további \(M\) sora rendre \(U_i\), \(V_i\) számpárokat tartalmaz. Egy ilyen számpár megfelel egy \(\{U_i, V_i\} \in E\) irányítatlan élnek. Egy él csak egyszer szerepel a fájlban.
- A bemenet feldolgozására javasoljuk a 3. feladat gráf beolvasó függvényének módosítását. Figyeljünk arra, hogy most a fájl első sorában nem szerepelnek az \(S\) és \(T\) csúcsok. Mivel a gráf élei nincsenek irányítva, érdemes lehet az éleket mindkét végpontjuk éllistájába felvenni.
- A fájl első sorában az \(N\), \(M\) természetes számok találhatóak szóközökkel elválasztva, ahol
- A program második bemenete egy egész számokból álló számsor. A program feladata eldönteni, hogy a számsor tanú-e arra, hogy a gráfban található Hamilton-kör.
- Amennyiben a tanú megfelelő, a
tanu
amennyiben nem, akkor a
nem tanu
szöveget írjuk ki.
- Próbáljuk ki a programot a graf.text gráffal és az alábbi (tanújelölt) bemenetekkel:
Fájlnév Elvárt kimenet t1.text Tanu t2.text Nem tanu t3.text Nem tanu t4.text Nem tanu t5.text Tanu t6.text Nem tanu t7.text Nem tanu
6. Euklideszi algoritmus
Határidő: 2019-04-07 24:00
- Az euklideszi algoritmus segítségével két szám legnagyobb közös osztója hatékonyan meghatározható. Tudjuk, hogy ha \(a, b \in \mathbb{Z}^+\) a bemeten kettes számrendszerben van megadva, akkor a bemenet hossza \(O(\log a + \log b)\), az euklideszi algoritmus pedig \(\mathop{\mathrm{lnko}}(a, b)\) értékét legfeljebb \(O(\log a + \log b)\) lépésben meg tudja határozni.
- Az euklideszi.py fájlban megadtunk egy olyan kódrészletet, ami a matplotlib Python csomag segítségével kirajzolja a \(\log a + \log b\) függvény hőtérképét (heat map) az \((a, b)\) koordinátasíkon, úgy, hogy \(a\) és \(b\) értéke \(1\) és \(100\) közötti egész legyen. A hőtérkép a szivárvány színeivel jelzi a számok nagyságát, a matplotlib csomag régebbi változatában alapértelmezésben az ibolyakék a kicsi, a vörös a nagy számoknak felel meg, az újabb verzióikban a színek csak a sárgáig változnak.
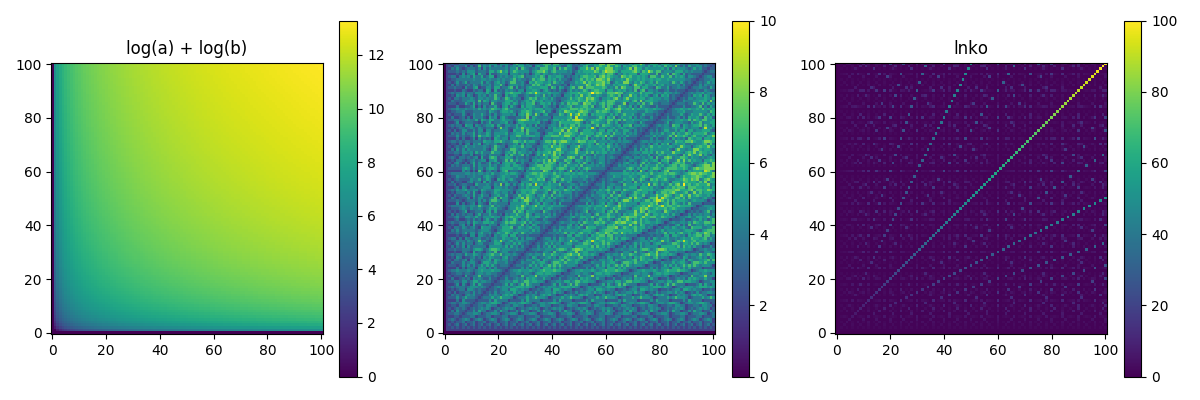
- Módosítsuk a programot úgy, hogy bemutassa az euklideszi algoritmus futását! Jelenítsünk meg három hőtérképet, egymás mellett egy ablakban, az alábbiak valamelyikéhez hasonlóan. Az eredmény a matplotlib újabb verziójában
régi verziójában
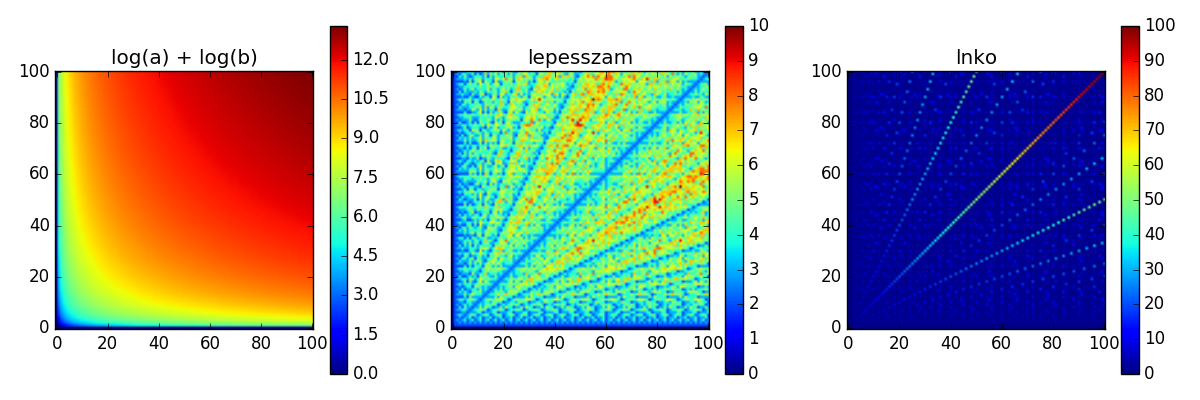
A hőtérképeken az alábbi függvények legyenek láthatóak:
- Az első hőtérkép mutassa a \(\log_2 a + \log_2 b\) függvényt, ezt generálja a kiadott programkód.
- A második hőtérképen ábrázoljuk az euklideszi algoritmus lépésszámát az egyes \((a, b)\) párokon. Számoljuk meg, hány lépést tesz meg az euklideszi algoritmusban szereplő rekurzió, azaz hányszor végzünk maradékos osztást az \((a_i, b_i)\) párral, vagy döntünk a leállás mellet.
- Végül a harmadik hőtérkép mutassa \(\mathop{\mathrm{lnko}}(a, b)\) értékét.
- Több ábra megjelenítéséhez használható a matplotlib subplot függvénye. Ennek argumentuma egy \(nmk\) alakú háromjegyű szám, ami az ábra pozícióját határozza meg. Ennek jelentése: a rajzvásznat \(n \times m\) részre osztjuk, és a továbbiakban ezek közül a \(k\)-adik részre rajzolunk, ahol a \(k=1\) a bal felső részábra indexe. Így például a
plt.subplot(132)hívás vízszintesen három részre osztja a vásznat, és a középső részre rajzolja a további plt hívások eredményeit.
7. Nyers erő
Határidő: 2020-04-16 24:00
- Az NP-teljes problémák megoldásának egy lehetséges módszere a „nyers erő” alkalmazása. Ebben a megközelítésben generáljuk a bemenethez tartozó összes lehetséges tanút, és egyesével ellenőrizzük őket. Ha találunk egy jó tanút, akkor a bemenet benne van a vizsgált nyelvben, míg ha egyetlen generált tanú sem volt jó, akkor a bemenet biztosan nem eleme a nyelvnek. Természetesen ettől az eljárástól sem remélhetjük, hogy a feladatot polinom időben oldja meg.
- A \(\textrm{FGTLN}\) nyelv az olyan \((G, k)\) párokból áll, ahol a \(G\) egyszerű irányítatlan gráfban van pontosan \(k\) elemű független ponthalmaz. Arra, hogy \((G, k) \in \textrm{FGTLN}\), jó tanú egy \(k\) elemű \(F \subseteq V(G)\) független ponthalmaz. Ha \(|V(G)| = n\), akkor az \(F\) halmazról \(O(n^2)\) időben eldönthető, hogy egyetlen \(u, v \in F\) pontpár között sem húzódik él a gráfban.
- Készítsünk olyan programot, ami a parancssori argumentumként kapott fájlban leírt \((G, k)\) párról eldönti, hogy a \(\textrm{FGTLN}\) nyelvben van-e. Ha találtunk \(k\) elemű független halmazt, akkor írjuk ki az elemeit is a standard kimenetre. Ellenkező esetben jelezzük, hogy a gráfban nincs \(k\) elemű független halmaz.
- A maxftl.py fájlban megadtuk a grafot_olvas függvényt, ami beolvassa a parancssori argumentumként megadott fájlból \(G\) gráf éllistáját és a \(k\) számot. A beolvasott fájl formátumát és a függvény visszatérési értékét a függvény forráskódjának docstring megjegyzésben dokumentáltuk.
- Generáljuk a gráf \(\{0, 1, \ldots, n - 1\}\) csúcsainak \(k\) elemű kombinációit, és vizsgáljuk meg, hogy független ponthalmazt alkotnak-e. Ha az \(F\) kombináció független ponthalmaz, akkor írjuk ki az elemeit a standard kimenetre, és állítsuk le a keresést. Ha egyetlen kombináció sem független, akkor jelezzük, hogy nem találtunk \(k\) elemű független halmazt.
- Segítségképp a kombinaciok függvényben megadtunk egy kódrészletet, amely az itertools csomag segítségével a standard kimenetre írja a \(\{0, 1, \ldots, 9\}\) halmaz összes 3 elemű részhalmazát.
- Próbáljuk ki a programot az alábbi fájlokkal! Azokhoz a bemenetekhez, melyek a \(\textrm{FGTLN}\) nyelvben vannak, megadtunk egy független ponthalmazt is példaként a kimenetre. Természetesen más független halmaz is elfogadható jó tanúnak.
Fájl Független halmaz ftln1.text 1 2 7 ftln2.text nincs ftln3.text 0 4 9 11 12 14 19 ftln4.text nincs ftln5.text 2 5 18 29 39 ftln6.text nincs
8. Egészértékű lineáris programozás
Határidő: 2020-04-22 24:00
- Az NP-teljes problémák megoldásának egy másik ismert módszere az, hogy a problémát visszavezetjük egy másik, jól ismert NP-teljes problémára. Ha a jól ismert problémára rendelkezésünkre áll egy hatékony heurisztikus megoldó, akkor általában jobb eredményt tudunk elérni, mint a nyers erővel.
- A feladatban egészértékű lineáris programozás (EP) segítségével oldjuk meg az előző hétről ismerős FGTLN problémánál kicsit általánosabb MAXFGTLN problémát. Ebben nem egy adott \(k\) méretű, hanem egy maximális méretű független halmazt keresünk. Az egészértékű lineáris programot a PuLP Python csomag segítségével oldjuk meg. A csomag a Python beépített pip, illetve pip3 csomagkezelőjével a
pip install pulp
paranccsal telepíthető.
- A pulppelda.py fájlban megadtunk egy egyszerű példaprogramot, ami a \begin{align*} \max\, x_0 + x_1,\\ \text{ahol } x_0, x_1 \in \mathbb{Z},\\ x_0 \ge 0, \\ x_1 \ge 0, \\ 2 x_0 + x_1 \le 10, \\ x_0 + 2 x_1 \le 10 \end{align*} egészértékű programozási feladat egy megoldását a standard kimenetre írja. Tanulmányozzuk a programot! A megértéshez segítséget nyújthat a PuLP csomag dokumentációja.
- Készítsünk programot a MAXFGTLN probléma megoldására!
- Olvassuk be a probléma bemenetét, azaz a \(G\) irányítatlan gráfot és a \(k\) számot az előző feladatból megismert formátumú fájlból, bár \(k\) értékét itt nem fogjuk használni. A program az előző feladathoz hasonlóan a fájl nevét parancssori argumentumként fogja megkapni.
- Fogalmazzuk meg a MAXFGTLN problémát egészértékű programozási feladatként.
- Programozzuk le az egészértékű programozási feladatot a PuLP csomaggal, és hívjuk meg rá a megoldót. (Ügyeljünk arra, hogy mind a feladatnak, mind a feladatban szereplő változóknak egyedi szöveges nevet kell adni, mert ezekkel hivatkozik a probléma elemeire a PuLP, amikor átadja őket a külső megoldónak. Ha a változók nevei nem egyediek, akkor hibajelzést fogunk kapni.)
- Írjuk ki a maximális méretű független halmaz méretét és egy ilyen halmaz elemeit a standard kimenetre. A PuLP a célfüggvény értékét nem egész, hanem lebegőpontos számként adja vissza. Mivel az egész szám, kiírás előtt kerekítsük.
- Futtassuk le a programot az előző feladatban kiadott bemenetekkel! Bár most többet követelő feladatot oldunk meg, a páros indexű fájlokon látható, hogy mennyivel gyorsabb az egészértékű programozás, mint a nyers erő. (Valójában a múlt heti feladatban is meghatároztuk a maximális független halmaz méretét, mivel két-két gráf azonos volt, de az egyikben \(k\) méretű független létezett, míg a másikban egy annál 1-gyel nagyobb méretű már nem.)
9. Ládapakolás
Határidő: 2020-04-29 24:00
- A ládapakolás feladatban a bemeneten megadott \((s_i)_{i = 1}^n\), \((0 < s_i \le 1)\) súlyokról kell meghatározzuk, hogy minimálisan hány \(1\) kapacitású ládába férnek el. A probléma NP-teljes, így hatékony megoldás (jelenlegi ismereteink szerint) nem áll rendelkezésre, ám számos közelítő algoritmus született rá. Ebben a feladatban néhány közelítő heurisztika vizsgálata lesz a cél.
- A ladak.py fájlban megadtunk egy olyan keretprogramot, ami egy fix bemeneten vizsgál egy alsó korlátot és három közelítő algoritmust a ládapakolás problémára:
- Az OPT értéke a tárgyak összsúlyának felső egészrésze, ami egy alsó korlát a szükséges ládák számára.
- Az előadáson tanult FF algoritmus minden tárgyat az első olyan ládába teszi, ahol az elfér.
- A szintén tanult FFD algoritmus hasonló az FF-hez, ám előbb csökkenő sorrendbe rendezi a tárgyakat.
- A BF (best-fit) heurisztika minden tárgyat abba a ládába helyez el, ahol a legkevesebb szabad hely marad.
- Módosítsuk a ladak.py fájlt és fejezzük be a program elkészítését!
- Valósítsuk meg a first_fit_pakol függvényben az FF algoritmust.
- Valósítsuk meg az ffd_pakol függvényben az FFD algoritmust. Ügyeljünk arra, hogy a Python a listákat referencia szerint adja át, így ha a súlyokat tartalmazó listát rendezzük, az a hívó által átadott listát közvetlenül módosítja. Ehelyett inkább dolgozzunk a lista egy másolatával.
- A fix targyak lista helyett állítsunk elő (a program minden futtatásakor más) 1000 elemű, 0 és 1 közötti súlyokat tartalmazó listát, és hívjuk meg ezzel a pakoló függvényeket.
- Futtassuk néhányszor a programot! Mit tapasztalunk, hogy működnek a közelítő algoritmusok a generált véletlen bemeneteken?
10. Akrobaták
Határidő: 2020-05-06 24:00
- Cirkuszi akrobaták egymás vállára állva minél nagyobb tornyot szeretnének létrehozni (a toronyban minden szinten csak egy akrobata lesz). Esztétikai és gyakorlati szempontok miatt egy ember vállára csak olyan állhat, aki nála alacsonyabb és könnyebb is. Feladatunk, hogy meghatározzuk a lehetséges legtöbb emberből álló toronyban található emberek számát.
- Az akrobata.py fájlban megadtunk egy példaprogramot, ami beolvassa az akrobatákat a parancssori argumentumban megadott nevű fájlból, majd magasság szerint nemnövekvő sorrendben kiírja őket a standard kimenetre. A fájl formátuma a következő:
- A fájl első sorában egyetlen pozitív egész szám szerepel, az akrobaták \(N\) darabszáma.
- A következő \(N\) sorban \(M_i\) \(S_i\) számpárok szerepelnek. A fájl \(i + 1\). sorában szereplő számpár rendre az \(i\). akrobata magasságát és súlyát adja meg.
- Az akrobaták beolvasásáról az akrobatakat_beolvas függvény gondoskodik, mely az Akrobata osztály példányait tartalmazó listával tér vissza. Az akrobaták rendelkeznek az azonosito, magassag és suly tulajdonságokkal, valamint egy raallhat metódussal, mely megadja, hogy egy akrobata ráállhat-e egy másikra.
- Dinamikus programozás segítségével határozzuk meg az akrobatákból a szabályok szerint építhető legtöbb emberből álló toronyban található emberek számát! Az elkészült programot próbáljuk ki az alábbi bemeneteken, melyekhez megadtuk azt is, hány emberből áll a legtöbb embert tartalmazó torony:
Bemenet Maximális torony cirkusz1.text 2 cirkusz2.text 3 cirkusz3.text 1 cirkusz4.text 100 cirkusz5.text 15 cirkusz6.text 37
11. Intervallumok uniója
Határidő: 2020-05-13 24:00
- Adott a számegyenesen \(N\) zárt intervallum, \([A_1, B_1], [A_2, B_2], \ldots [A_N, B_N]\), ahol \(A_i\) és \(B_i\) természetes számok. Szeretnénk meghatározni az intervallumok összhosszát, vagyis az \(\bigcup_{i = 1}^N [A_i, B_i]\) halmaz mértékét.
- Az intervallum.py fájlban megadtunk egy példaprogramot, ami beolvassa az intervallumokat a parancssori argumentumban megadott nevű fájlból. A fájl formátuma a következő:
- Az első sorban egyetlen természetes szám található, az intervallumok \(N\) száma.
- A következő \(N\) sorban szereplő \(A_i\) \(B_i\) számpárok határozzák meg az intervallumok határait, ahol \(0 < A_i < B_i\).
- Az intervallumokat_olvas függvény a megadott fájlból Intervallum objektumok listáját olvassa be. Az Intervallum osztálynak két tulajdonsága van, a kezd kezdőpontja és veg végpontja.
- Egészítsük ki az osszhossz függvényt úgy, hogy kiszámítsa az intervallumok összhosszát! Törekedjünk a hatékony, \(O(N \log N)\) lépésszámú megvalósításra.
- Próbáljuk ki a programot az alábbi bemeneteken. A hatékony, \(O(N \log N)\) lépésszámú algoritmus az alábbi bemenetek mindegyikén lefut néhány másodperc alatt. A bemenetek mellett megadtuk az intervallumok összhosszát is.
Bemenet Összhossz interv1.text 9 interv2.text 596 interv3.text 6541 interv4.text 94581377 interv5.text 632741470
12. Bináris keresőfa
Határidő: 2020-06-20 24:00
- Ebben a feladatban egy bináris keresőfa adatszerkezetet fogunk készíteni. A binfa.py programban megadtuk a keresőfa implementációjának egy részét.
- A bináris fát a BinarisFa osztály reprezentálja. A fa gyökere a gyoker tagváltozóban van tárolva. Ha a fa üres, ennek értéke None, egyébként a gyökér a FaCsucs osztály egy példánya.
- A csúcsok a FaCsucs osztály példányai. A bal és jobb tagváltozók értéke vagy None, ha az adott gyerek nem létezik, vagy a gyerekcsúcsot reprezentáló FaCsucs példány.
- A fához tartozó műveletek a BinarisFa osztály beszur, keres, szintszam és preorder_nyomtat metódusai. Ezek ellenőrzik, hogy van-e a fának gyökere, majd továbbhívnak a FaCsucs osztály megfelelő, rekurzióval megvalósított metódusaira.
- A beszur és keres műveletek közös rekurzív része a FaCsucs csucsot_keres metódusa. Ez bejárja a fát a paraméterül kapott értéket keresve, és visszaadja azt a csúcsot, ahol a bejárás elakad. Ez vagy az a csúcs, amelyik tartalmazza a keresett értéket, vagy ha az érték nincs a fában, akkor az a csúcs, melynek az új értéket tartalmazó csúcs a közvetlen gyereke kell legyen.
- A főprogram egész számokat olvas be parancssori argumentumként megadott nevű fájlból, majd beszúrja őket a bináris fába. Ezután preorder sorrendben a standard kimenetre írja a fában tárolt értékeket, és kiszámítja a fa szintjeinek a számát.
- Egészítsük ki a binfa.py programot az implementáció hiányzó részével!
- A BinarisFa beszur metódusában szúrjuk be a kapott értéket a fába. Ehhez segítségül hívhatjuk a FaCucs csucsot_keres metódusát, amely azt a csúcsot adja vissza, amely vagy tartalmazza a keresett értéket, vagy a keresett értéket a csúcs közvetlen gyerekeként kell beszúrni. Ennek a metódusnak a használatát mutatja be a BinarisFa keres metódusa is. Ügyeljünk arra, hogy a beszúrás üres bináris fán is működjön, illetve olyanon is, amely már tartalmazza a beszúrni kívánt értéket. Az utóbbi esetben a beszúrás idempotens.
- A FaCsucs preorder_nyomtat metódusában írjuk ki a fa csúcsait rekurzió segítségével preorder sorrendben a standard kimenetre.
- A FaCsucs szintszam metódusában szintén rekurzió segítségével határozzuk meg a fa szintjeinek a számát.
- Az elkészült programot próbáljuk ki a binfa1.text fájlban található bemenettel! Más bemenetekre hogyan viselkedik a program?