A tárgy célja a Valószínűségszámítás 1 című tárgy tematikájához kapcsolódó programozási feladatok megoldásán keresztül a hallgatók programozási képességeinek szinten tartása, és egyúttal a valószínűségszámítás alapfogalmainak véletlen események szimuláción keresztül való jobb megértésének elősegítése.
A tárgy 1 kredites, ami összesen 30 óra, azaz heti 2-3 óra programozási munka elvégzését kívánja. Olyan feladatokat igyekszünk adni, melyek érdekesek lesznek mindenki számára, és amelyek megoldása sok haszonnal fog járni. A feladatok száma 12, összpontszáma 50. Követelmény a feladatok határidőre való leadása (illetve a pontszám 20%-ának elvesztése mellett legföljebb 1 héttel későbbi, késedelmes leadása) és a feladatokra kapható maximális összpontszám legalább 50%-ának elérése. A hibásan megoldott feladat az eredmény kihirdetése utáni 1 héten belül javítható. A feladatok megoldását a valszam.prog@gmail.com címre csatolmányként kell elküldeni, külön fájlban a Python programkódot, és ha van, külön fájlban az adatokat. A programfájl neve a feladat sorszámával kezdődjön, folytatásul a hallgató neve legyen szóközök nélkül, pl. Kovács Jutka 5-dik házi feladatát 5KovacsJutka.py, adatfájlját 5adatKovacsJutka.txt néven küldje el. Ha Python3-ban oldja meg, a program nevének vége 3 legyen, példánkban 5KovacsJutka3.py. A levél tárgya 5. HF, az esetleges javításé 5. HF javítás legyen. Minden házi feladat kísérő levelébe az alábbi szöveget kell írni:
E programot magam kódoltam, nem másoltam vagy írtam át más kódját, és nem adtam át másnak. Kovács Jutka
Az, hogy az otthoni feladat kódját mindenkinek magának kell beírnia, programkódot átadnia, mástól kérnie és elfogadnia nem szabad, nem zárja ki az együtt gondolkodás vagy a segítségkérés lehetőségét! Konzultáció is kérhető, személyes is.
Táblázat
Az eredmények táblázata itt van.
Tartalomjegyzék
- Monthy Hall háromajtós problémája (17-09-20, 5 pont)
- Szentpétervári paradoxon (17-09-27, 3 pont)
- Binomiális eloszlás (17-10-04, 6 pont)
- Diszkrét valószínűségi változókat kezelő osztály (17-10-14, 4 pont)
- Bertrand-paradoxon (17-10-21, 5 pont)
- Indul a parti (17-10-28, 4 pont)
- Adott eloszlásfüggvényű véletlen számok generálása (17-11-01, 3 pont)
- Buffon-féle tűprobléma (2017-11-08, 3 pont)
- U súlyfüggvényű kocka konvolúciója (2017-11-19, 4 pont)
- Feltételes függetlenség (2017-11-26, 5 pont)
- Többdimenziós normális eloszlás (2017-12-03, 5 pont)
- Zipf-törvény (2017-12-10, 3 pont)
Feladatok
1. feladat: Monthy Hall háromajtós problémája (határidő 2017-09-20 szerda 24:00, 5 pont)
- Egy egykori televíziós játék (USÁ-ban Let's Make a Deal volt a címe és Monthy Hall volt a műsorvezető, Magyarországon Zsákbamacska néven futott) utolsó fázisában a játékost 3 csukott ajtó elé állítják, melyek egyike mögött egy értékes jutalom (pl. gépkocsi) van, míg a másik kettő mögött valami értéktelen. A játékos kiválaszt egy ajtót, de mielőtt azt kinyitnák, a műsorvezető a másik két ajtó közül egyet kinyit megmutatva, hogy nem ott van az értékes ajándék, és fölajánlja a játékosnak, hogy még meggondolhatja magát és megváltoztathatja a döntését, választhatja a másik ajtót. A kérdés az, hogy ilyenkor mit érdemes tennie a játékosnak:
- tartson ki eredeti döntése mellett, vagy
- változtassa meg döntését, vagy
- mindegy, pl. 0.5 valószínűséggel kitart eredeti döntése mellett, 0.5 valószínűséggel megváltoztatja.
Írjunk programot, mely szimulálja e játékot 3000-szer. A program
- véletlen módon jelöljön ki egy ajtót, amely mögött az értékes ajándék van,
- a játékos szerepében véletlenül válasszon egy ajtót (nem tudva az előző választásról),
- a műsorvezető szerepében (véletlenszerűen) válasszon egy ajtót, mely különbözik a játékos által választottól és amely mögött nem az értékes jutalom van,
- a játékos szerepében a 3000 eset közül az első 1000-ben maradjon meg az eredeti döntése mellett, a második 1000 esetben változtassa meg döntését, a harmadik 1000 esetben 0.5 valószínűséggel változtasson eredeti döntésén, végül
- eredményül írjuk ki a játékos nyerésének relatív gyakoriságát mindhárom esetben szóközzel elválasztva.
- A feladat célja: a relatív gyakoriság szimuláción keresztül való megtapasztalása és a feltételes valószínűség fogalmának előkészítése egy paradoxonnak tűnő problémán keresztül.
- Programozási cél: szimuláció programozása, véletlen szám generálása, ciklus írása.
- Segítség: a random csomag betöltésével (import random) és a random.random() hívással egy 0 és 1 közé eső véletlen számot kapunk (egyenletes eloszlás szerint). Az int(random.random()*3) hívás a 0, 1 vagy 2 értéket adja vissza.
- A Python 2-ben – mi ezt tanultuk – egészek osztása egész eredményt ad. Python 3-ban ez megváltozott. Python 2-ből kérhetőek a jövő (a 3-as) egyes új tulajdonságai, például az osztás e tulajdonsága megváltoztatható a kód elejére írt from __future__ import division paranccsal.
- A feladat a példatárban 2.20 sorszámmal szerepel.
2. feladat: Szentpétervári paradoxon (határidő 2017-09-27 szerda 24:00, 3 pont)
- Egy érmével addig dobunk, míg a fej oldalára nem esik. Ha ez az \(n\)-edik feldobáskor történik meg, akkor a játékos \(2^n\) forintot nyer (ld. Wikipédia). Szimuláljunk \(m\) játékot (azaz \(m\) fej dobásig játszunk). Mennyi a nyeremény átlaga \(m=100\), \(m=10000\) és \(m=1000000\) esetén?
- A program kimenete e három átlag szóközzel elválasztva.
- A feladat célja egy végtelen várható értékű valószínűségi változóval való tapasztalatszerzés.
- A feladat a példatárban 3.21 sorszámmal szerepel.
3. feladat: Binomiális eloszlás (határidő 2017-10-04 szerda 24:00, 6 pont)
- Az e heti feladatban három oszlopdiagramot kell kirajzolni egyetlen ábrában. Az első ábra egy \((n,p)\) paraméterű binomiális eloszlás valószínűségeloszlását mutatja, a második ábra e binomiális eloszlást szimulálva tapasztalati valószínűségeloszlást mutat, míg a harmadik ábra a binomiális eloszlást közelítő \(\lambda=n\cdot p\) paraméterű Poisson-eloszlás valószínűségeloszlásának első \(n+1\) oszlopát ábrázolja.
- A program eredményeként valami hasonló ábrát fogunk kapni (a színek, skálázás,... nem lényeges része a feladatnak):
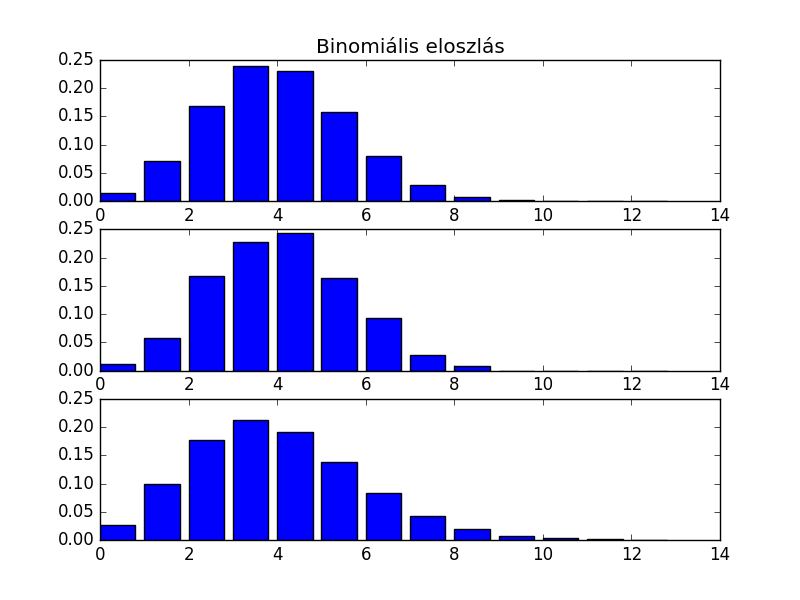
- A program bemenete \(n\), \(p\), \(k\), ahol \(n\) és \(p\) a binomiális eloszlás paraméterei, és \(k\) a szimulációk száma. A program például parancssorból így indítható:
python 3KovacsJutka.py 12 0.3 1000
vagy Python 3 esetén:
python3 3KovacsJutka3.py 12 0.3 1000
Ehhez a sys modult kell betölteni, ekkor az első paramétert a sys.argv[1] tartalmazza karakteres formában, tehát számoláshoz még konvertálni kell. (A kész programot futtassuk le különböző számhármasokon, pl. 20 0.05 1000, 40 0.02 1000 vagy 40 .5 1000.)
- A binomilás eloszlás értékeinek listájához a binomiális együtthatókra szükség lehet, amihez a math modul használható. Az első ábrán oszlopdiagramokkal ábrázoljuk a valószínűségeloszlást.
- A binomiális eloszlás szimulációja megvalósítható úgy, hogy $n$ kísérletet végzünk egy $p$ valószínűségű esemény bekövetkezéseinek számára. A valószínűségi változó értéke $m$, ha az esemény az $n$ kísérletből $m$-szer következett be. Ezt az $n$ kísérletet $k$-szor megismételjük, így a valószínűségi változó $k$ értékét kapjuk. A második diagram $m$-edik oszlopa $i/k$ magas legyen, ha a valószínűségi változó $i$-szer vette föl az $m$ értéket. (A feladat e pontja egyszerű ciklusokkal és a random modul random függvényével megvalósítható, de a numpy.random.binomial függvény is használható.)
- A harmadik ábra egy Poisson-eloszlású $X$ valószínűségi változó első $n+1$ értékét mutatja, ahol \[ P(X=m)=\frac{\lambda^m}{m!}e^{-\lambda}, \quad m=0, 1, 2,\dots, \] ahol $\lambda=np$.
- Az ábrák kirajzolásához a matplotlib csomag használható. Érdemes egy kis időt eltölteni megismerésével: nagyon egyszerűen használható. Betöltése a import matplotlib.pyplot as plt paranccsal történik, ami után
plt.bar(lista1,lista2,oszlopszelesseg) plt.show()
egy olyan oszlopdiagramot rajzol ki, ahol az oszlopok bal alsó sarkának $x$-koordinátája a lista1-ben, az oszlopok magassága a lista2-ben, az oszlopok szélessége az oszlopszelesseg változóban van. Ha három részábrát akarunk egyben ábrázolni, akkor az első előtt egy
plt.subplot(311)
parancsot kell kiadni, ahol a 311 jelentése: 3 sorban 1 oszlopban az első részábra jön. A következőbe 312, az utolsóba 313 kerül. (E három részdiagram „hasonlítani fog egymáshoz”.)
4. Diszkrét valószínűségi változókat kezelő osztály (határidő 2017-10-14 szombat 24:00, 4 pont)
- Írjunk egy Drv (dicrete random variable) nevű osztályt a véges értelmezési tartományú diszkrét valószínűségi változók kezelésére. Az osztály konstruktora két azonos hosszúságú listát vár, az első az $X$ valváltozó $x_k$ értékeit, a második a $p_k=\mathbb{P}(X=x_k)$ valószínűségeket tartalmazza. Írjuk meg a következő metódusokat:
- __init__: konstruktor.
- e: $X$ várható értéke.
- is_nonneg: igaz értéket ad vissza, ha a valószínűségi változó nem negatív, egyébként hamis.
- reweighting: a 4.1 feladat általánosításaként visszaad egy $Y$ valószínűségi változót, mely az eredeti $X$ valószínűségi változóból a következő ,,átsúlyozással'' kapható: \[\mathbb{P}(Y=x_k)=\frac{x_kp_k}{\mathbb{E}(X)},\] feltéve hogy $X$ nemnegatív és nem azonosan 0.
- __repr__: (Nem kötelező) a valváltozó megjelenítéseként kiírja az $(x_k,p_k)$ párokat, illetve közülük az első 20-at, ha $X$ értelmezési tartománya 20-nál több elemű.
- Binomial: A Drv leszármazott osztálya, a binomiális eloszlás. Paraméterei \(n\) és \(p\). Ebben az osztályban írjuk újra az e és az is_nonneg metódusokat.
- Uniform: egyenletes eloszlású valváltozót adó osztály, a Drv leszármazott osztálya, paramétere \(n\), értékeinek listája \([1,2,\dots,n]\). Itt is írjuk újra az előbb említett metódusokat.
- A kód megírása után egy példa az osztály használatára ipythonban:
In [2]: y = Drv( [40, 33, 25, 50], [1/4]*4 ) In [3]: y.xk Out[3]: [40, 33, 25, 50] In [4]: y.pk Out[4]: [0.25, 0.25, 0.25, 0.25] In [5]: y.is_nonneg() Out[5]: True In [6]: y.e() Out[6]: 37.0 In [7]: x = y.reweighting() In [8]: x.xk Out[8]: [40, 33, 25, 50] In [9]: x.pk Out[9]: [0.2702702702702703, 0.22297297297297297, 0.16891891891891891, 0.33783783783783783] In [10]: x.e() Out[10]: 39.28378378378378 In [11]: z = Binomial(5, .4) In [12]: z.xk Out[12]: [0, 1, 2, 3, 4, 5] In [13]: z.pk Out[13]: [0.077759999999999982, 0.25919999999999999, 0.34560000000000002, 0.23040000000000005, 0.076800000000000021, 0.010240000000000003] In [14]: z.e() Out[14]: 2.0 In [15]: z = Uniform(3) In [16]: z.xk Out[16]: [1, 2, 3] In [17]: z.e() Out[17]: 2.0 In [18]: z # nem kötelező Out[18]: (1,0.333333333333) (2,0.333333333333) (3,0.333333333333)
- Néhány segítség: tanulmányozzuk a class, super, all utasításokat, jól jön a listaértelmezés, binomiális együtthatóhoz a from scipy.misc import comb.
5. feladat: Bertrand-paradoxon (határidő 2017-10-21 szombat 24:00, 5 pont)
- A Bertrand-paradoxon (valójában nem paradoxon) arra példa, hogy egy látszólag egyszerű valószínűségi változó milyen sokféleképp valósítható meg, ha a definíciója nem elég egyértelmű. E paradoxon klasszikus változata azt kéri, hogy számítsuk ki annak valószínűségét, hogy egy adott körbe véletlenül berajzolt húr mekkora valószínűséggel lesz rövidebb, mint a körbe rajzolható egyenlő oldalú háromszög oldala (ld. Wikipédia). Paradoxonnak azért tűnik e probléma, mert három különböző, egyaránt józan feltevés mellett az $1/2$, a $2/3$ és a $3/4$ is helyes válasz lehet.
- Az első feltevés az, hogy választunk egy véletlen irányt (ez szimmetria okokból lehet bármelyik, így akár a vízszintes is) és a húrt a rá merőlegesek közül választjuk ki, véletlenül választva egy pontot a kör vízszintes átmérőjén.
- A második feltevés az, hogy választunk a kör kerületén egy pontot és a húr másik végpontja a kör kerületének egy másik, véletlenül választott pontja lesz.
- A harmadik feltevés az, hogy választunk a körlapon (egyenletes eloszlás szerint) egy pontot, és azon keresztül húzunk egy húrt úgy, hogy az merőleges legyen a pontot a középponttal összekötő egyenesre.
Mindhárom feltevést és a megoldást is (kicsit más megfogalmazásban) ötletes és élvezetes animációkkal szemlélteti az MIT egy oldala (a megoldás elolvasása előtt érdemes kicsit töprengeni rajta!)
A továbbiakban legyen a kör egységsugarú, tehát az átmérője 2, és jelölje a húr hosszát egy kísérletben $X$, azaz $X$ egy valószínűségi változó, melynek értéke $0$ és $2$ közé esik. A feladat az lesz, hogy írjunk egy bertrand(N) paranccsal hívható függvényt, mely mindhárom modellben szimulál $N$ kísérletet a húr kiválasztására, följegyzi a hosszakat egy listába, és annak alapján kirajzolja mindhárom esetben a tapasztalati eloszlásfüggvényt. A tapasztalati eloszlásfüggvény értéke az $x$ helyen azt mondja meg, hogy mennyi a relatív gyakorisága az $\{X\lt x\}$ eseménynek. E függvény lépcsős függvény. (Az eloszlásfüggvényt becsüljük vele, melynek definíciója $F_X(x)=\mathbb P(X\lt x)$.) Ha például három kísérletet végezve a húrok hossza $1.5$, $0.4$ és $1.2$, akkor a tapasztalati eloszlásfüggvény ábrája így néz ki (tekintsünk el a lépcsős függvénybe berajzolt függőleges szakaszoktól, és a szakadási helyeken gondoljuk a lépcsős függvényt balról folytonosnak):
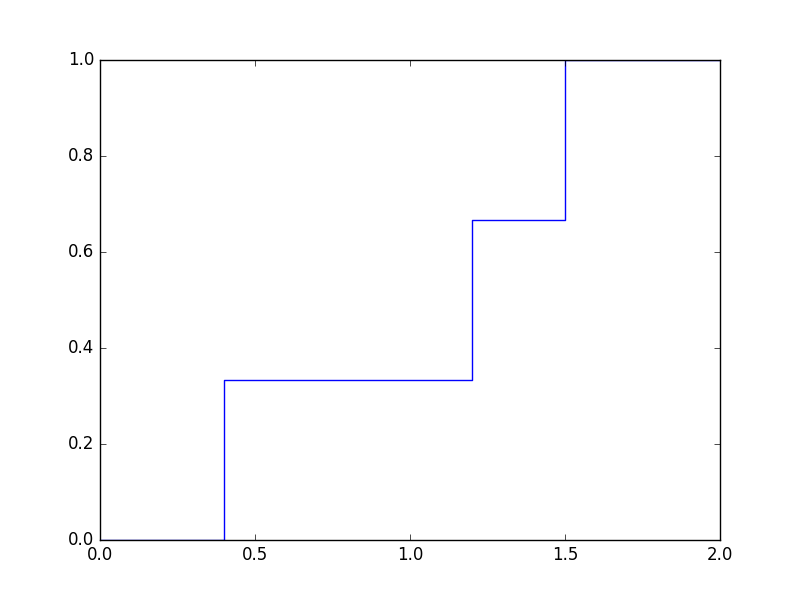
A feladat kimenete legyen a három tapasztalati eloszlásfüggvény grafikonja egyetlen ábrán. A függvényeket elég a $[0,2]$ intervallum fölött ábrázolni. Nyilván mindhárom függvény monoton növekvő, értéke $0$-ban $0$, $2$-ben $1$, és a paradoxon megoldásából tudjuk, hogy a $\sqrt3\approx1.732$ helyen közelítőleg $1/2$, $2/3$, illetve $3/4$ a modelltől függően.
- Segítség a megoldáshoz (nem kell követni a tanácsokat, de segíthetnek):
- Az első modellhez: válasszunk egy véletlen $r$ számot a $[-1,1]$ intervallumból, és számítsuk ki az $(r,0)$ pontba állított, $x$-tengelyre merőleges húr hosszát (ehhez a math modul acos és sin függvényei kellenek).
- A második modellhez: legyen az egyik pont az $(1,0)$, a másik pont legyen a kör kerületének egy véletlen pontja, azaz $(cos\alpha,\sin\alpha)$, ahol $\alpha$-t válasszuk egyenletes eloszlás szerint a $[0,2\pi)$ intervallumból (itt ki kell számítani e két pont távolságát).
- A harmadik modellhez: válasszunk először egy tetszőleges pontot a $[-1,1]\times[-1,1]$ négyzetből (azaz válasszunk két véletlen számot a $[-1,1]$ intervallumból, és képezzünk belőlük számpárt), és ellenőrizzük, hogy a körbe esik-e. Ha nem, válasszunk még egyet addig, míg egy körbe esőt nem találunk. Ha találtunk, az origótól való távolságából az első modellhez hasonlóan számolható a húr hossza.
- A tapasztalati eloszlásfüggvény kirajzolásához: ha szimuláltunk $N$ kísérletet, egy sort() metódussal rendezzük, írjunk az elejére egy $0$-t, végére egy $2$-est. Ez a lista adja a rajz vízszintes tengelyén a beosztásokat, amely pontok felett a lépcsős függvény „ugrik”. Minden egyes ilyen helyen a függvény értéke $1/N$-nel nő. Ha a legrövidebb húr hossza $r$ (ez $1$ valószínűséggel nagyobb $0$-nál), akkor a függvény a $[0,r]$ intervallumon $0$, így a függvényértékek listáját érdemes $y=[0,0,1/N,2/N,...,1]$-nek választani. A kirajzoláshoz a plt.step(x,y) függvény használható, ahol $x$ és $y$ az előbb konstruált két lista. (E Python függvény a grafikonba függőleges vonalakat is berajzol.) Egy megoldást mutat a következő ábra $N=1000$ esetén:
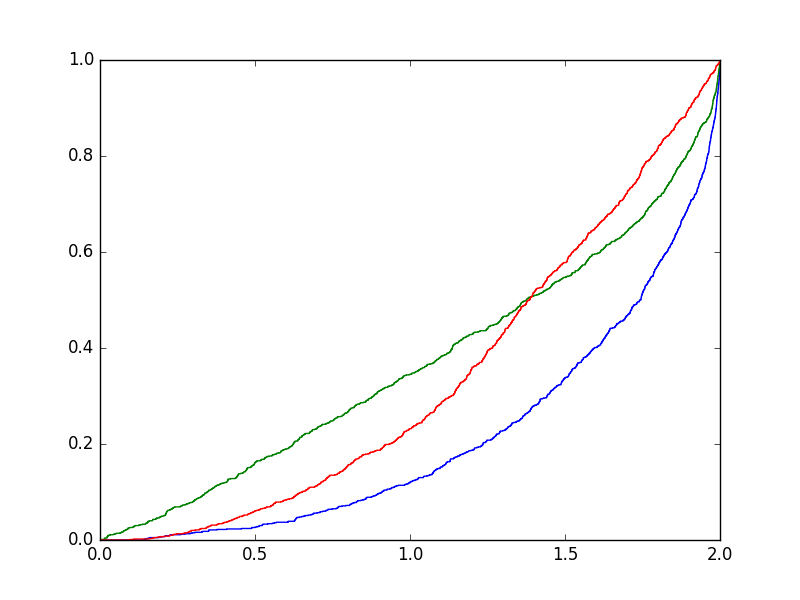
- A program elkészülte után végezzünk kísérleteket különböző $N$ értékekkel és cseréljük ki a step függvényt plot-ra.
- A feladat célja a következő fogalmak megértésének elősegítése: folytonos valószínűségi változó, eloszlásfüggvény és annak tapasztalati közelítése.
6. feladat: Indul a parti (határidő 2017-10-28 szombat 24:00, 4 pont)
- Móricka este 10 órára egy bulit szervez, meghívja 10 barátját. Egy különleges játékot talált ki amihez rajta kívül legalább 8 emberre van szükség. Mindenki izgatott, így amint befut a 8-adik barátja már kezdik is a játékot. Tegyük fel, hogy a barátai egymástól függetlenül 10 és 11 óra között egyenletes eloszlás szerint érkeznek (beleértve azt is, hogy 10 előtt senki sem érkezik, viszont 11-ig mindenki befut). Jelölje \(X\) azt, hogy a 10 és 11 közötti időintervallum hányad részénél kezdődik a játék (vagyis \(X\) egy 0 és 1 közötti értéket felvevő valószínűségi változó).
- Írjunk egy \(X\)-et szimuláló függvényt!
- Tekintsük a következő két sűrűségfüggvényt: \begin{align*} f_a (x)&= \frac{10!}{7! \cdot 2!}x^7 (1-x)^2,\quad 0\le x \le1\\ f_b (x)&= \frac{10!}{6! \cdot 3!}x^6 (1-x)^3,\quad 0\le x \le1. \end{align*}
Szimuláljuk \(X\) értékét 5000-szer, ezekből rajzoljuk meg a hisztogramot 50 oszloppal, és a két sűrűségfüggvényt, majd ennek alapján döntsük el, hogy közülük melyik lehet \(X\) sűrűségfüggvénye!
- Felhasználva az előzőleg generált 5000 adatot, \(X\) mindegyik szimulált értékét helyettesítsünk be mindkét sűrűségfüggvénybe és a helyettesített értéket szorozzuk meg egymástól és minden korábbi valószínűségi változótól független, \([0,1]\)-en egyenletes eloszlású véletlen számmal. Végül ezeket az értékeket pontokként ábrázoljuk az eredeti szimulált értékek függvényében. Egy ábra két részábráján legyen a két függvényhez tartozó ,,pontfelhő''. Döntsük el a két ábra alapján, hogy a két lehetőség közül melyik \(X\) sűrűségfüggvénye! A választ indokoljuk is!
- A feladat kimenete két ábra. Az elsőn két \([0,1]\)-en értelmezett függvény grafikonja, és egy 50 oszlopból álló hisztogram látható. A második ábra két részábrából áll, a fölsőn az első sűrűségfüggvény alatti területet fedő ponthalmaz, az alsó részábrán a második sűrűségfüggvény alatti területet fedő ponthalmaz látható. A kísérőlevélben adjunk rövid magyarázatot arra, hogy a második ábráról hogyan és miért olvasható le, hogy melyik lehet a valódi sűrűségfüggvény.
- Segítség, tanácsok:
- Függvény grafikonjának kirajzolásához a következő kódot lehet használni (más jó megoldás is van!):
from __future__ import division import numpy as np import matplotlib.pyplot as plt # t egy olyan tömb lesz, mely a 0, .02, .04,... 1 számokat tartalmazza lepeskoz = 1/50 t = np.arange(0, 1 + lepeskoz, lepeskoz) plt.plot(t, sfv(t), color = "red")
Itt a plot függvény első argumentuma az értelmezési tartomány értékeit, a második argumentum a hozzájuk tartozó értékeket adja meg, ahol sfv a sűrűségfüggvény, amit előtte definiálni kell.
- A hisztogram kirajzolása azt jelenti, hogy egy intervallum fölé olyan magas oszlopot rajzolunk, mely arányos az intervallumba esett szimulált értékek számával. Ennek kirajzolására van egyszerű függvény, ahol kiserletek az \(X\) értékeinek listája, bins az intervallumbeosztás, normed azt jelenti, hogy az oszlopok összterülete mennyi legyen:
plt.hist(kiserletek, bins=t, normed=1)
- A pontok rajzolásához meg kell adni a plt.plot harmadik argumentumaként, hogy milyen stílusú legyen, oda elég egy "r." sztringet írni, ami azt jelenti, hogy a megadott pontok nem lesznek összekötve, és a pontfelhő színe piros lesz (r=red).
- Függvény grafikonjának kirajzolásához a következő kódot lehet használni (más jó megoldás is van!):
- A feladat célja a sűrűségfüggvény szemléltetése és a béta eloszlás szimulációja. Programozási cél: elemi programozási és grafikai ismeretek gyakorlása.
7. feladat: Adott eloszlásfüggvényű véletlen számok generálása (határidő 2017-11-01 szerda 24:00, 3 pont)
- Egy \(X\) valószínűségi változó eloszlásfüggvénye a \([0,2]\) intervallumon a következő: \(F_X(x)=x^2\), ha \(x\in[0,0.5]\), és \(F_X(x)=(x+1)/3\), ha \(x\in(0.5,2]\). Írjunk Python függvényt, mely szimulál egy ilyen eloszlásfüggvényű valószínűségi változót, azaz amely minden meghívására visszaad egy \(F_X\) szerinti véletlen számot. Írjunk programot, mely \(1000\) ilyen véletlen számot generál, és kiírja ezek átlagát, és azt, hogy az \(1000\) szám között hány volt egyenlő \(0.5\)-del.
- A feladat célja valószínűségi változó függvényének, például az $F_X(X)$ valószínűségi változónak a megértése, és ezt használva adott eloszlású valószínűségi változó szimulálása.
8. feladat: Buffon-féle tűprobléma (határidő: 2017-11-08 szerda 24:00, 3 pont)
- A Buffon-féle tűprobléma egy klasszikus feladat, megismerhető például Vetier András jegyzetének 28. oldalán. Ezt fogjuk általánosítani. Vegyünk egy megfelelően nagy papírt, amelyen egymástól egyenlő (például egységnyi) távolságra párhuzamos egyenesek vannak. Egy \(L\) hosszúságú tűt véletlenszerűen dobjunk a papírra. Legyen \(X\) a tű által metszett egyenesek száma. Írjuk ki \(N\) kísérlet alapján \(X\) tapasztalati súlyfüggvényének értékeit a 0, 1, 2, …, \(\lfloor L\rfloor+1\) helyeken.
- A program parancssori bemenete egy pozitív egész \(N\) szám és egy pozitív valós \(L\) szám, kimenete egy \(\lfloor L\rfloor+2\) számból álló számsorozat.
- Megjegyezzük, hogy ha \(L=0.5\), akkor a kísérletet fizikailag sokszor elvégezve a metszés relatív gyakoriságának reciproka \(\pi\)-t közelíti (amennyire a fizikai korlátok ezt lehetővé teszik).
- A szimuláció szimmetria okok miatt többféleképp is egyszerűsíthető. Például a fent említett jegyzetbeli gondolatot követve a tű egyenesekkel bezárt hegyes szögét és középpontjának a közelebbi egyenestől való távolságát tekinthetjük a \([0,\pi/2]\), illetve a \([0,0.5]\) intervallumon egyenletes eloszlásúnak. Próbálkozhatunk úgy is, hogy a tű ,,bal'' végpontját a \([0,1]\) intervallumon egyenletes eloszlásúnak tekintjük, stb.
- Akik szeretik a kihívásokat megpróbálkozhatnak az elméleti levezetéssel valamely konkrét \(L\) esetén (pl. \(L=2\) vagy \(L=5\)) kiszámítva az egyes metszésszámok elméleti valószínűségét, majd a végeredményt összevethetik a tapasztalati értékekkel.
9. feladat: U súlyfüggvényű kocka konvolúciója (határidő: 2017-11-19 vasárnap 24:00, 4 pont)
- Egy cinkelt kocka úgy van súlyozva, hogy az $1$, $2$, $3$, $4$, $5$, $6$ értékek rendre $0.35$, $0.10$, $0.05$, $0.05$, $0.15$, $0.30$ valószínűségekkel adódnak. Számoljuk ki (ne szimuláljuk hanem a konvolúciós képletet használva pontosan számoljuk ki) egy, kettő, három, négy, tíz és húsz kockadobás összegének eloszlását, majd ábrázoljuk a súlyfüggvényeket. A húsz kockadobás összegéhez tartozó ábrára másik színnel rajzoljuk rá az összeget jól közelítő normális eloszlás sűrűségfüggvényét is.
- A feladat célja: Konvolúció számolása, a centrális határeloszlás-tétel szemléltetése.
- Segítség: $k$ darab kocka súlyfüggvényének konvolúciója egy $6^k$ méretű adathalmazból is meghatározható, azonban az így megírt program nem fog tudni a határidő előtt lefutni. Tanácsom az, hogy $k$ súlyfüggvény konvolúcióját rekurzívan számolják: 2 kockáé egy $6\times6$-os mátrix diagonálisan összegzett értékeiből kapható meg, ahol a valószínűségeloszlás 11 elemű. 3 kocka esetén ezt a súlyfüggvényt konvoláljuk a kocka súlyfüggvényével, amihez egy $6\times11$-es mátrix diagonális összegei használhatók, stb.
10. feladat: Feltételes függetlenség (határidő: 2017-11-26 vasárnap 24:00, 5 pont)
Legyen \(W=(X,Y,Z)\) háromdimenziós valószínűségi változó véges sok lehetséges értékkel. Jelölje a lehetséges értékek halmazát rendre \(\mathcal{X}\), \(\mathcal{Y}\), \(\mathcal{Z}\). Azt mondjuk, hogy \(X\) és \(Y\) valószínűségi változók a \(Z\) valószínűségi változóra nézve feltételes(en) függetlenek ha minden \(z\in \mathcal{Z}\)-re az \((X,Y)\mid Z=z\) feltételes eloszlás előáll az \(X\mid Z=z\) és \(Y\mid Z=z\) felételes eloszlások szorzataként. Ez alatt azt értjük, hogy minden \(x \in \mathcal{X}\) és \(y \in \mathcal{Y}\) esetén \[ \mathop{\text{P}}(X=x,Y=y\mid Z=z)=\mathop{\text{P}}(X=x\mid Z=z)\cdot\mathop{\text{P}}(Y=y\mid Z=z). \] (Szükség esetén további információ a Wikipédián.)
- Az egyszerűség kedvéért tegyük fel, hogy \(\mathcal{X}=\mathop{\rm range}(i)\), \(\mathcal{Y}=\mathop{\rm range}(j)\) és \(\mathcal{Z}=\mathop{\rm range}(k)\) valamely \(i,j,k\in \mathbb{N}^+\) egészekre, ahol \(\mathop{\rm range}(n)=\{0,1,\dots,n-1\}\). Így az \(X\), \(Y\), \(Z\) valószínűségi változók megadásához elég a valószínűségek egy listáját megadni. A \(W\) megadásához egy háromdimenziós tömb megadására lesz szükség. Ehhez listák listájának listája vagy a numpy csomag array függvénye használható (utóbbi esetben sok kényelmes metódussal). A feladat az lesz, hogy számítsuk ki
- az \(X\), \(Y\), \((X,Y)\) marginálisokat (azok eloszlását),
- adott \(z\)-re az \(X\mid Z=z\) és \(Y\mid Z=z\) eloszlásokat (lista vagy 1-dimenziós tömb).
- adott \(z\)-re az \((X,Y)\mid Z=z\) feltételes eloszlást (listák listája, vagy 2-dimenziós tömb),
továbbá döntsük el, hogy
- \(X\) és \(Y\) függetlenek-e,
- \(X\) és \(Y\) a \(Z\)-re nézve feltételesen függetlenek-e.
- A feladat a fenti függvények meghívásával egy olyan feltfuggetlenseg nevű függvény megírása, mely
- beolvas egy 3-dimenziós eloszlást, és
- kiírja a három marginális eloszlását, a három feltételes marginális eloszlást mindegyik lehetséges \(z\) értékre, és két logikai értéket.
Ezután futtassuk le a programot az alábbi két eloszlásra!
- Definiáljuk \((X,Y,Z)\)-t a következőképpen. Legyen \(Z\) \(\frac{1}{2}\) valószínűséggel \(0\), \(\frac{1}{2}\) valószínűséggel \(1\). A \(Z=0\) feltétel mellett legyenek \(X\) és \(Y\) függetlenek úgy, hogy mindkét változó \(\frac{99}{100}\) valószínűséggel \(0\) és \(\frac{1}{100}\) valószínűséggel \(1\). A \(Z=1\) feltétel mellett legyen \(X\) és \(Y\) továbbra is független, de most mindkét változó a \(0\)-t vegye fel \(\frac{1}{100}\) valószínűséggel és az \(1\)-t \(\frac{99}{100}\) valószínűséggel. A konstrukcióból világos, hogy \(X\) és \(Y\) valószínűségi változók a \(Z\) valószínűségi változóra nézve feltételesen függetlenek. A feladat az, hogy a megírt függvények mindegyikét teszteljük ezen a háromdimenziós valószínűségi változón. (Látni fogjuk, hogy \(X\) és \(Y\) nem függetlenek.)
- Legyen most \((X,Y,Z)\) a következő. \(X\) és \(Y\) legyenek függetlenek úgy, hogy mindketten a \(0\) és \(1\) értékeket \(\frac{1}{2}\)-\(\frac{1}{2}\) valószínűséggel veszik fel. Legyen \(Z=X\cdot Y\). A feladat az, hogy a megírt függvényeket teszteljük ezen a háromdimenziós valószínűségi változón is (látni fogjuk, hogy \(Z\)-re nézve \(X\) és \(Y\) nem feltételesen függetlenek).
11. feladat: Többdimenziós normális eloszlás (határidő: 2017-12-03 vasárnap 24:00, 5 pont)
- E feladatunk a többdimenziós és az egydimenziós normális eloszlás egy fontos kapcsolatát szemlélteti. A feladat az, hogy állítsunk elő 1000 darab adott várható értékű, adott kovarianciamátrixú 2-dimenziós normális eloszlású pontot és ábrázoljuk őket a síkon. Az előállítást kétféleképp is meg kell valósítani! Először két független normális eloszlású párjából képzett vektorváltozó lineáris transzformációjával, amihez a numpy.random csomag normal függvénye használható (és pl. a numpy.linalg csomag). A transzformáció mátrixát jelölje \(\mathbf M\), ekkor a kovarianciamátrix \(\mathbf{M}\mathbf{M}^T\) lesz. Másodszor a numpy.random csomag multivariate_normal függvényével generáljuk a véletlen pontokat. E függvény argumentumai közt a kovarianciamátrix is szerepel. Végül mindkét ábrára rajzoljuk ki azt az ellipszist is, mely az adatok nagy részét tartalmazza. Az ellipszis félnagytengelyei a kovarianciamátrix szinguláris értékeinek 6-szorosai legyenek (a szinguláris érték itt a kovarianciamátrix pozitív szemidefinit volta miatt egybe esik a sajátérték négyzetgyökével). Az egyszerűség kedvéért a várható érték 0, illetve \((0,0)\) legyen.
- A program parancssorból fusson, parancssori bemenete a transzformációmátrix 4 eleme legyen sorfolytonosan megadva, kimenete két ábra. Például a python 12VargaLaszlo.py 2 5 3 0 bemenetre a program eredményeként a \[ \begin{bmatrix}2&5\\3&0\end{bmatrix} \] transzformációmátrixszal számolva a következőhöz hasonló két ábrát kapunk:
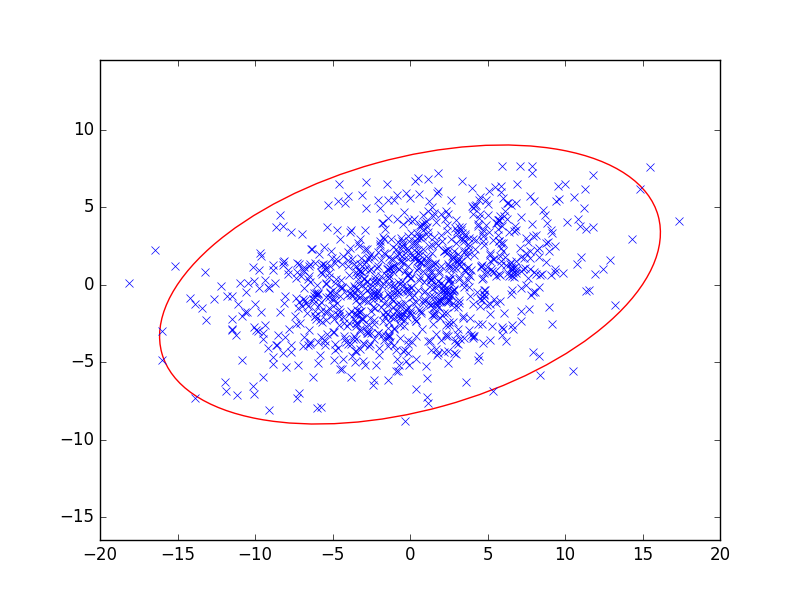
- Az ellipszis kirajzolása nehézséget okozhat. Ehhez a tengelyek mérete és a nagytengely hajlásszöge szükséges, aminek kiszámításához a np csomag rad2deg és arctan függvényei is használhatók. Néhány ötlet (nem kell követni, más út is lehetséges):
from matplotlib.patches import Ellipse # csomag a rajzoláshoz
ax = plt.subplot(111, aspect='equal') # egyetlen részábra
ell = Ellipse(xy=(0,0),... # kitöltendő
ell.set_facecolor('none') # legyen üres
ax.add_artist(ell)
plt.plot(x, y, 'x') # ezek már a pontok
plt.axis('equal')
- A feladat célja a 2-dimenziós normális eloszlás kovarianciamátrixának és a független normális eloszlásokból álló vektorváltozó lineáris transzformáltja kapcsolatának szemléltetése.
12. feladat: Zipf-törvény (határidő: 2017-12-10 vasárnap 24:00, 3 pont)
Az utolsó feladat egy érdekes megfigyelésről szól, a Zipf-törvényről, melyről a Wikipedia a következőt írja: „A Zipf-törvény azt állítja, hogy egy természetes nyelv egyes részeiben egy szó előfordulási gyakorisága fordítottan arányos a gyakorisági (előfordulási) táblában levő rangjával. Így, a leggyakoribb szó közel kétszer gyakoribb, mint a második leggyakoribb szó, és háromszor gyakoribb, mint a harmadik helyen lévő, stb.”
Amennyiben e szabály fennáll egy szövegre, akkor a gyakorisági függvény grafikonja egyenes egy olyan koordinátarendszerben ábrázolva, melyben mindkét koordinátatengely beosztása logaritmikus. A feladat az lesz, hogy egy természetes szövegre ellenőrizzük e szabályt grafikusan, azaz rajzoljuk ki a gyakoriságokat loglog koordinátarendszerben. Teszteléshez néhány szövegminta található a http://sandbox.hlt.bme.hu/~gaebor/zipf/ oldalon. E szabályt tökéletesen megvalósítja a szövegminták közt található tokeletes.txt fájl. Kisebb minták vannak az ember tragédiájából és nagyobb méretű angol szövegek.
A program kódolásához ezúttal (az utolsó hétre való tekintettel) nagy segítséget adunk, a program kódjának nagy részét mellékeljük, csak a hiányzó kódot kell pótolni. Hogy mit kell csinálni, az kitalálható a környezetből és a megjegyzésekből. A kód úgy van megírva, hogy Python és Python3 alatt egyaránt futtatható, de a Python kimenetében az ékezetes betűk utf8 kódja jelenik meg, Python3-ban olvashatóan maga a betű.
from __future__ import print_function # print meghivasa fuggvenykent
import matplotlib.pyplot as plt
import sys
filename = sys.argv[1]
def plot_zipf(filename):
d = {} # szotar
with open(.............) as f: # fájl megnyitása olvasásra
for line in f:
for word in line.strip().split(): # szavakra bont
word = word.strip(',.-_?! ').lower() # irasjelet torol
if word != '':
........... # a nem ures
# szavak szamolasa
# a szo a kulcs
# ertek a gyakorisag
data = sorted(d.values(), reverse=True) # a gyakorisagok
plt.loglog(range(..............), data) # kirajzolasa
plt.show() # loglog skalaval
# a szotar konvertalasa parok listajava, majd rendezese a
# a parok masodik eleme mint kulcs szerint, vegul az elso 10
# par kiirasa
print(sorted(d.items(), key=lambda x:x[1], reverse=True)[0:10])
plot_zipf(filename)
A kódot így, parancssorból futtatható alakban kérjük, de ha valaki a jupyter-ben ír és tesztel, betehet egy
%matplotlib inline
sort második sorként a kódba, de az elküldendő fájlból azt vegye ki!
- A feladat célja egy tapasztalati eloszlás megismerése, a megfelelő ábrázolás kiválasztása.
- Programozási cél: ismerkedés a természetes nyelvi adatok feldolgozásának alapjaival.